글을 시작하기에 앞서 해당 글은 Sanjoy Dasgupta, Christos Papadimitriou, Umesh 의 저서인 Algorithms를 참고하여 정리한 글임을 알려드립니다.
피보나치 입문
피보나치는 유명한 수열로 가장 많이 알려져있다. 수열 내에서 각 숫자들은 이전 두 숫자의 합이라는 것이 피보나치 수열의 원리이다. 피보나치수 $F_n$은 다음과 같다.
지수적 알고리즘
피보나치 수열은 $2^n$과 거의 같은 속도로 증가한다. 일반적으로 $F_n$≈$2^{0.694n}$ 이다. 따라서 피보나치 함수 fib(n)의 수행속도는 $2^{0.694n}$인 $(1.6)^n$에 비례한다. 즉, $F_n+1$을 계산하는 것은 $F_n$을 계산하는 시간의 1.6배가 더 걸린다는 것이다.
지수함수를 기반으로 한 피보나치 수열을 구하는 공식은 $n$에서 $0$이 될 때까지 스스로를 반복해야 하기 때문에 $n$이 크면 클수록 엄청나게 많은 시간이 소요된다. 그렇다면 좀 더 빠르게 만들 수는 없을까? 피보나치에서 나온 값들을 배열에 저장한다면, 더 빠르게 작동할 것이다.
다항 시간 알고리즘
다항함수는 지수함수보다 훨씬 빠르게 작동한다. 따라서 다항함수를 기반으로 작성된 코드가 훨씬 효율적이다. 코드는 먼저 $0$부터 $n$까지의 배열을 만든 후, 해당 배열의 인수를 다항식인 $f(X)=f(x-2)+f(x-1)$ 넣는 프로세스로 진행된다. 물론 $f(0)$과 $f(1)$은 $0$과 $1$로 값을 따로 지정한다. 이 방식은 지수함수를 기반으로 작성했을 때보다 훨씬 빠르고 효율적으로 작동한다.
좀 더 정확한 분석
위의 지수적 알고리즘과 다항 시간 알고리즘을 좀 더 정확하게 알아보고자 한다. 뒤의 1장에서 배우겠지만, $n$비트의 두 숫자를 더하는데 걸리는 시간은 $n$에 비례한다. 따라서 지수적 알고리즘은 $F_n$을 $n$의 수만큼 반복하여 더했기 때문에 연산 개수는 $n*F_n$이라고 할 수 있다. 또한 다항 시간 알고리즘의 연산 개수는 $n$의 개수에 따른 결과값들을 더하기 때문에 $n^2$에 비례한다. 정확하게 분석해도 다항시간 알고리즘이 훨씬 빠르다.
빅오 표기법 (big-O notation)
알고리즘의 효율성은 데이터 개수인 $n$에 따라 연산되는 횟수를 의미하며, 크게 ‘시간 복잡도(시간 효율성)’와 ‘공간 복잡도(공간 효율성)’로 나뉜다. 이런 알고리즘의 효율성을 나타내는 방법으로는 빅오(Big-O), 빅오메가(big-Ω), 빅세타(big-Θ) 표기법이 있다.
- 빅오(Big-O)표기법: 상한선 기준 (≤)
- 빅오메가(big-Ω): 하한선 기준 (≥)
- 빅세타(big-Θ): 상한선과 하한선 사이를 기준 (≤ ≤)
알고리즘 효율성은 그래프가 위로 향할수록(값이 클수록) 비효율적이라는 뜻이다. 빅오 표기법은 상한선을 기준으로 표기하기 때문에 알고리즘의 최악의 효율정도를 제시할 수 있어 주로 사용된다.
하지만 상한선이 꼭 해당 알고리즘의 최악의 효율성과 동일한 것은 아니다. 만약 최악의 효율성은 $n$값이 $1000$일 때 나타난다고 가정하자. 하지만 알고리즘은 찾고자 하는 값을 5번만에도 찿을 수 있다. 따라서 최악의 효율성이 항상 그 알고리즘의 효율성을 대변하지는 않는다.
빅오 표기법의 수학적 정의
빅오 표기법의 수학적 정의는 다음과 같다.
“모든 $n≥n_0≥0$ 에 대하여 $0≤f(n)≤c*g(n)$ 인 양수 $c$와 $n_0$가 존재하면 $f(n)=O(g(n))$이다.”
예를 통해 개념을 정리하자.
내가 만든 알고리즘의 시간 효율성을 나타내는 함수 $f(n)$이고 $n$과 상수 $c$을 아래의 방정식과 같다고 가정한다.
$f(n)=n^2+5n+8$
$g(n)=n^2+4$
위의 방정식은 $0≤f(n)≤c*g(n)$을 만족하는 상수 $c$가 존재한다.
또한 $n_0$은 $f(n)$와 $g(n)$가 같은 값일 때를 찾으면 되는데, 예시에서는 존재한다. 여기서 같은 값이란 그래프의 비교가 시작되는 지점이다. 상수 $c$와 $n_0$를 찾았다면 빅오 표기법으로 작성할 수 있다.
빅오 표기법의 특징
빅오 표기법은 몇 가지의 특징을 가지고 있다.
상수항을 무시한다.
빅오 표기법에서는 데이터 입력값인 $n$이 충분히 크다고 가정하며, 알고리즘의 효율성 또한 $n$값에 좌우되기 때문에 상수항처럼 사소한 부분은 무시한다.$O(3n^2)$ -> $O(n^2)$
영향력이 크지 않은 항도 무시한다.
빅오 표기법에서는 가장 영향력이 큰 항을 제외한 나머지는 큰 영향력이 없다. 따라서 제외하여 판단한다.$O(3n^2+5n+15)$ -> $O(n^2)$
아래의 그래프는 각 함수마다의 성능을 보여준다.
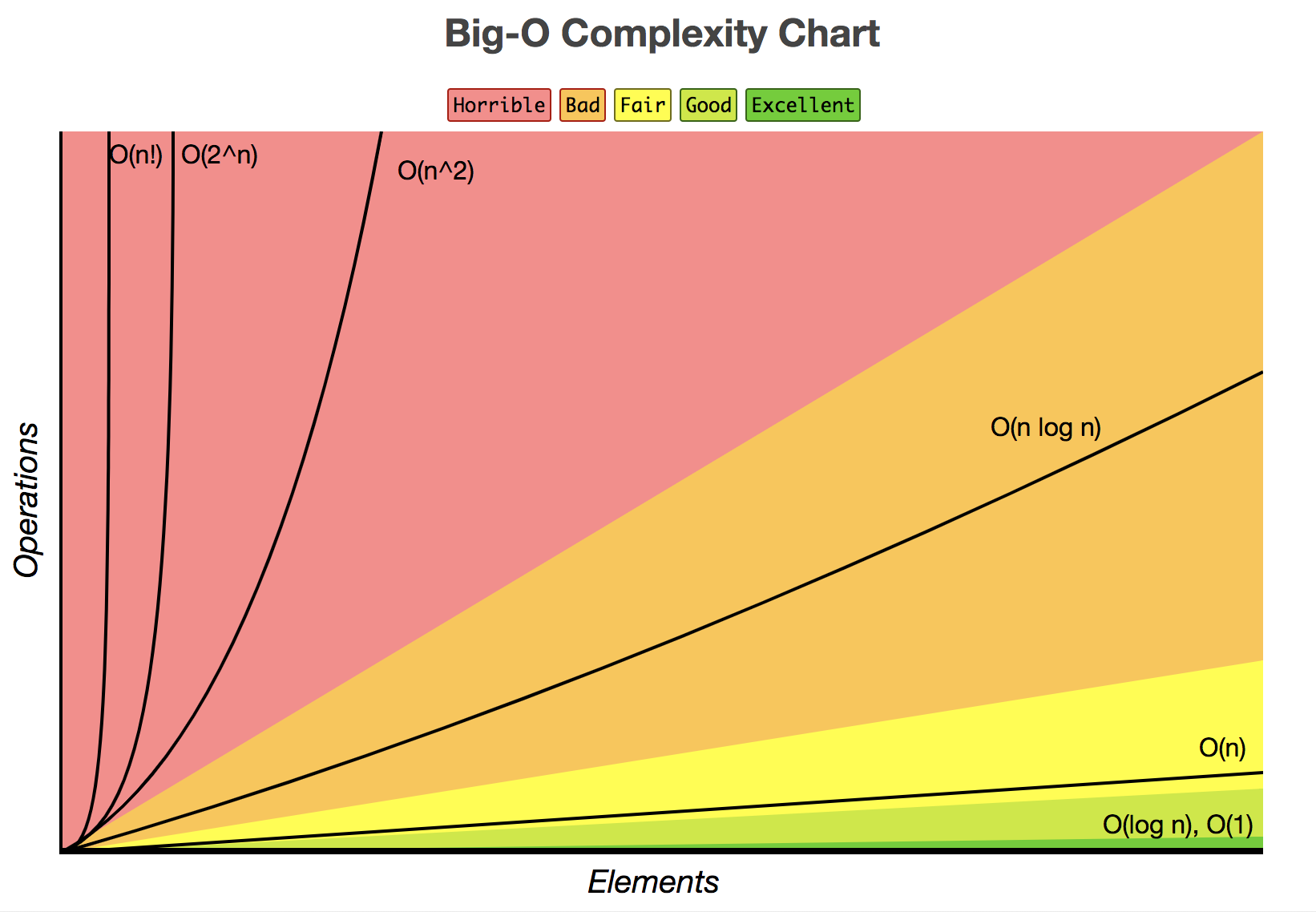
그래프에 나와있는 시간 효율성을 정리하면 다음과 같다.
$O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n)$
상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수
위의 순서를 보면, 상수함수가 가장 작고 지수함수가 가장 크다. 즉 상수함수는 데이터 수가 많아도 빠르게 작동하는 알고리즘이며, 지수함수는 데이터 수가 많아질수록 급격하게 느려지는 알고리즘이라는 뜻이다. 시간 효율성 관점에서는 상수함수가 더욱 우월하다.