2. 활성화 함수

해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.

활성화 함수

활성화 함수란 신경망 노드에 위치해 있는 함수로서 입력값들을 출력 신호의 여부로 변환해주는 함수이다. 보통 은닉층에서 사용하는 활성화 함수와 출력층에서 사용하는 활성화 함수로 나눠져 있으며, $h(x)$로 표기한다.

은닉층에서 사용하는 활성화 함수

은닉층에서 사용되는 기본적인 활성화 함수로는 3가지 정도가 있다.

계단 함수

계단 함수는 입력값이 $0$이하이면 $0$, $0$을 초과하면 $1$로 변환해주는 함수이다. 수식으로는 다음과 같다.

$h(x) = \begin{cases} 0 & \text{(x≤0) $$}\\ 1 & \text{(x>0) $$}\\ \end{cases}$

아래는 위 수식의 코드 구현이다.

function step_function(x)
    if x<=0
        return 0
    else
        return 1
    end
end

이를 그래프로 나타내보자.

Julia> using Plots
Julia> x = range(-5.0, 5.0, step = 0.1)
Julia> y = step_function.(x)
Julia> plot(x,y)

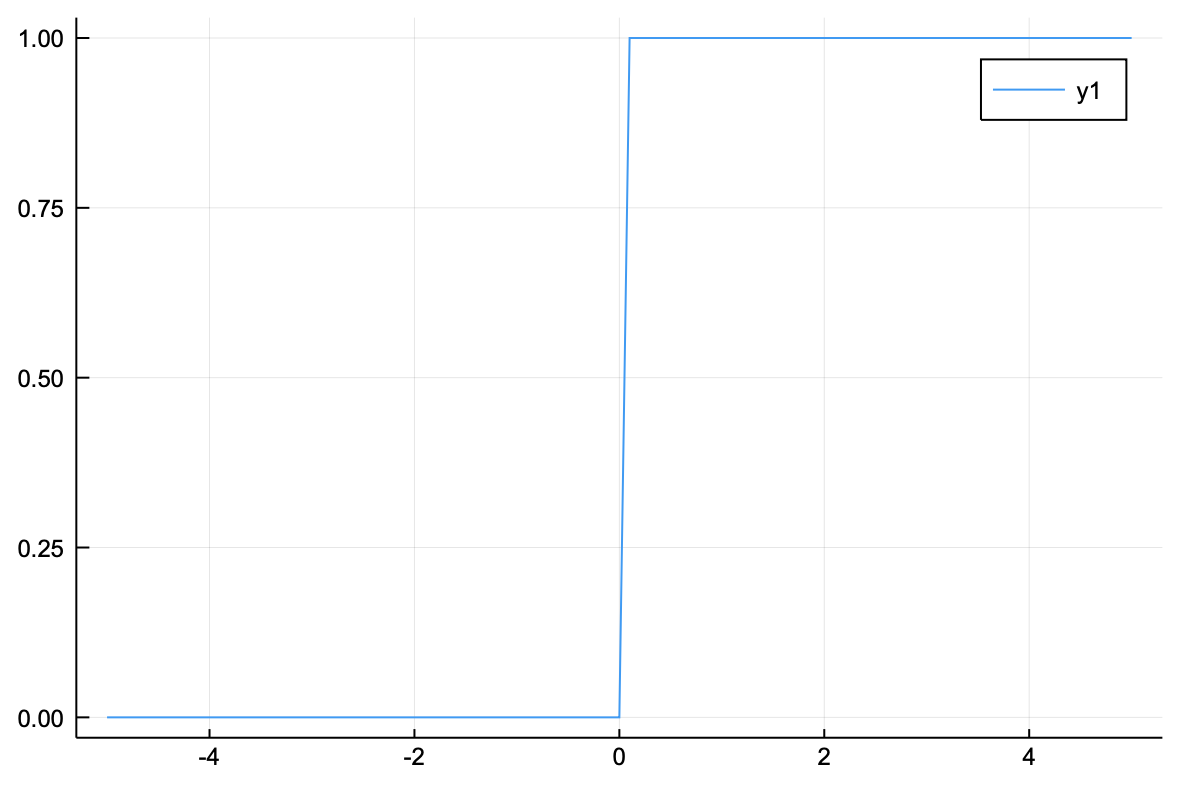
그래프에서 보면 $0$을 기준으로 $0$ 또는 $1$을 반환하는 것을 확인할 수 있다. 위의 함수는 연속적인 값이 아닌 이진수를 결과로 반환한다.

Tip
위의 코드를 보면 step_function.(x)에 도트 연산자를 확인할 수 있다. 도트 연산자는 배열 단위의 입력 값에 함수나 연산자를 각 요소별로 적용해준다.

시그모이드 함수

시그모이드 함수는 입력값들을 $0$과 $1$사이의 수로 변환해주는 함수이다. 수식은 아래와 같다.

$h(x)=\frac{1}{1+e^{-x}}$

위의 식을 코드로 구현해보자.

1
2
3

function sigmoid(x)
    return 1 / (1+exp(-x))
end

그래프를 그려보면 $0$과 $1$ 사이의 소수들로 구성된 것을 볼 수 있다.

Julia> using Plots
Julia> x = range(-5.0, 5.0, step = 0.1)
Julia> y = sigmoid.(x)
Julia> plot(x,y)

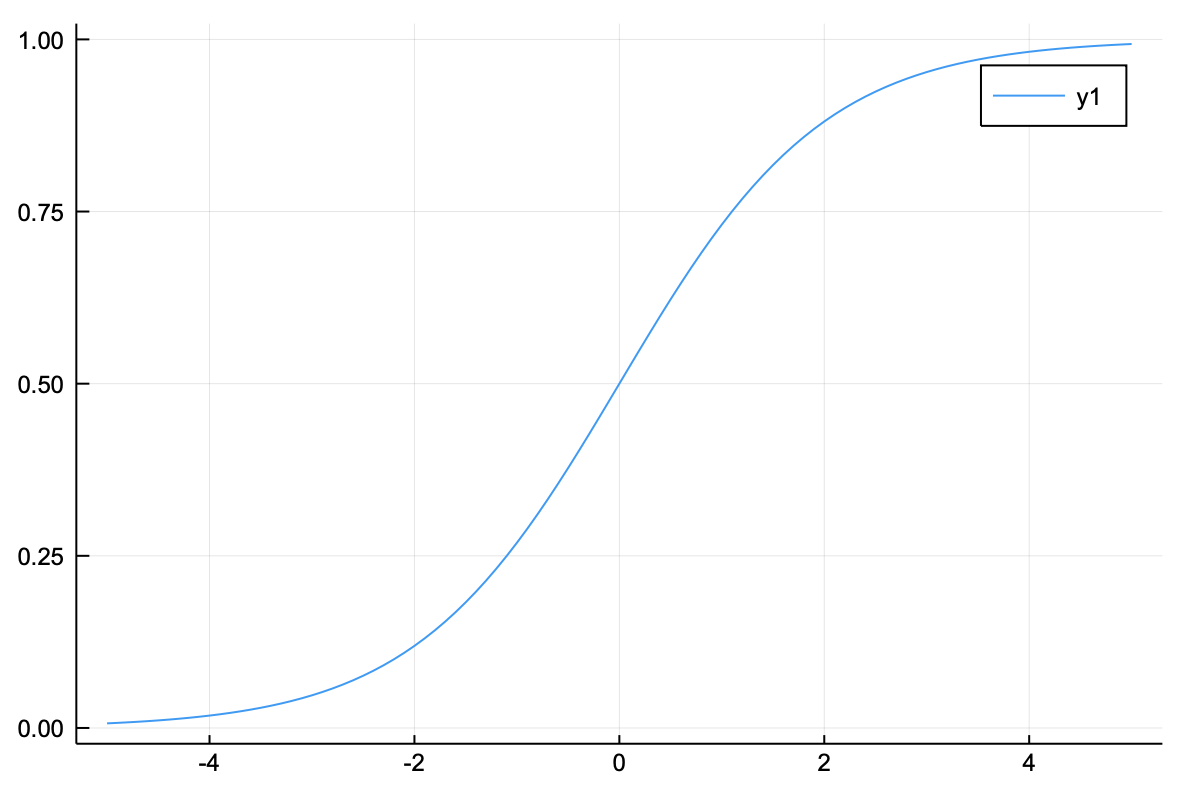
시그모이드 함수는 $0$과 $1$의 사이에서 연속적인 값을 반환하며, $0$을 중간값인 $0.5$로 설정한다. 따라서 계단 함수와 달리 각 신호의 강도를 표현할 수 있다.

ReLU 함수

ReLU 함수는 음수를 모두 $0$으로 바꾸고 양수는 그대로 출력하는 함수이다. 수식은 다음과 같다.

$h(x) = \begin{cases} 0 & \text{(x≤0)$$}\\ x & \text{(x>0) $$}\\ \end{cases}$

위 수식을 코드로 구현해보자.

1
2
3

function relu(x)
    return max(0,x)
end

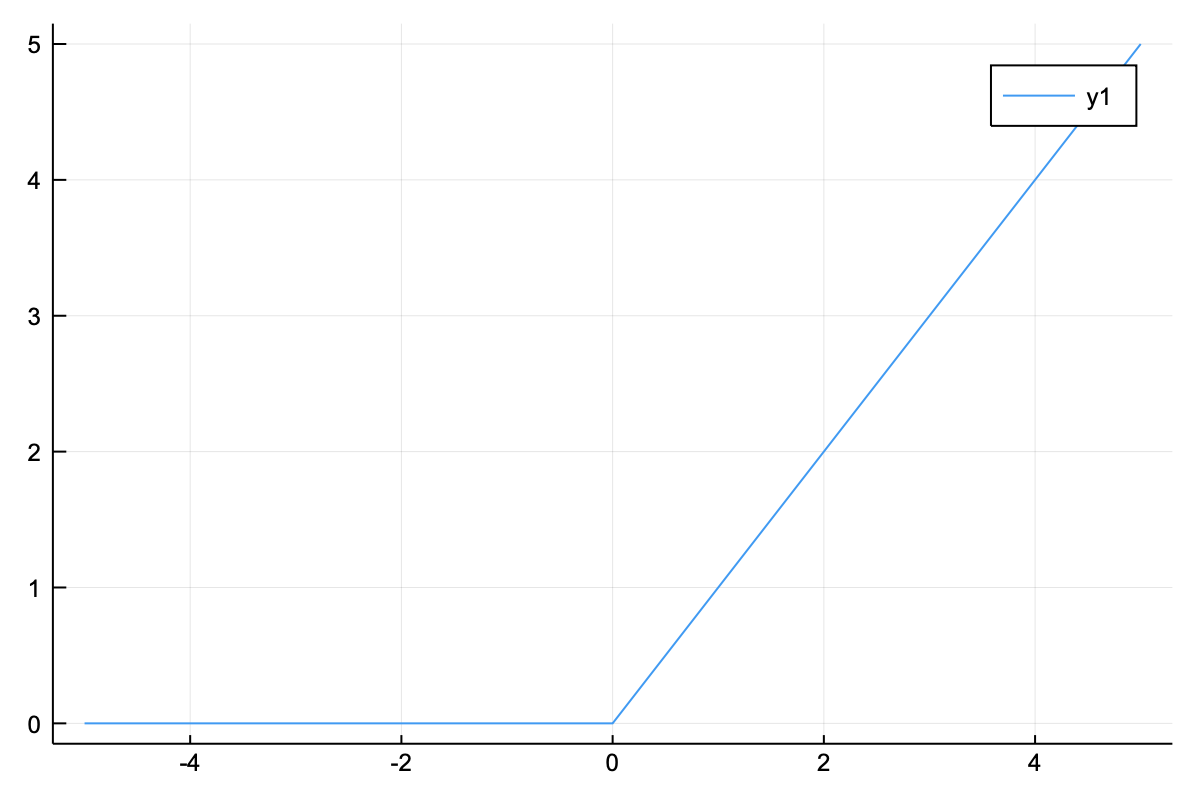
위의 그래프를 통해 음수는 모두 $0$으로 처리되며, 양수는 값이 그대로 출력되는 것을 확인할 수 있다.

세 가지 함수 비교

지금까지 은닉층에서 사용하는 활성화 함수들을 살펴보았다. 이제는 배열에 직접 적용해봄으로서 각 함수들을 비교해보고자 한다.

1	Julia> x = [-1 -2 -3;0 3 7]

위의 코드는 예시로 적용해 볼 $2\times3$ 배열이다. 계단 함수와 시그모이드 함수, ReLU 함수 순서로 적용해보자.

Julia> step_function.(x)
2×3 Array{Int64,2}:
 0  0  0
 0  1  1

계단 함수는 음수와 $0$은 모두 ‘$0$’으로 바꾸고 양수들을 ‘$1$’로 출력하였다.

Julia> sigmoid.(x)
2×3 Array{Float64,2}:
 0.268941  0.119203  0.0474259
 0.5       0.952574  0.999089

시그모이드 함수는 각 배열 요소들을 $0$부터 $1$까지의 수로 변환하여 출력하였다. 요소 중 하나인 $0$은 중간값 0.5로 설정된 것을 볼 수 있다.

Julia> relu.(x)
2×3 Array{Int64,2}:
 0  0  0
 0  3  7

ReLU 함수의 경우 음수는 모두 $0$으로 바꾸고 양수는 그대로 출력한 것을 확인할 수 있다.

출력층에서 사용하는 활성화 함수

출력층에서 사용되는 활성화 함수는 목적에 따라 달라진다. 일반적으로 회귀에는 항등 함수, 분류에는 소프트맥스 함수가 쓰인다.

항등 함수

항등 함수는 입력값을 그대로 출력한다. 수식과 코드는 아래와 같다.

$σ(x)=x$

1
2
3

function identity_function(x)
    return x
end

소프트맥스 함수

소프트맥스 함수는 0과 1사이의 값을 비율로 출력하기 때문에 “확률”로 해석할 수 있다. 이런 이유로 분류 신경망에서 소프트맥스 함수를 사용한다. 예를 들어, 꽃 사진 하나를 분석하여 어떤 꽃인지 분류하는 신경망을 구현 중이라면 소프트맥스 함수는 (장미 70%, 진달래 21%, 붓꽃 9%) 이런 식으로 결과를 제공한다. 수식은 다음와 같다.

$y_k=\frac{e^{a_k}}{\sum_{i=1}^n e^{a_i}}$

이 수식에서 $y_k$는 출력층의 $k$번째 노드이며, 분자의 $a_k$는 $k$번째 입력 값이다. 또한 분모에서 $n$은 총 출력층의 개수이며, 분모 전체는 출력된 값의 전체 합을 의미한다. 이를 코드로 구현하면 아래와 같다.

function softmax(x)
    c = maximum(x)
    exp.(x.-c)/sum(exp.(x.-c))
end

위 코드에서 입력 신호의 최대값을 빼는 이유는 오버플로(overflow) 문제를 막기 위함이다. 오버플로(overflow)란 결과값이 컴퓨터가 표현할 수 있는 값을 넘어갔을 때 발생하는 문제이며, 최대값을 빼주면 에러를 막을 수 있다.

두 가지 함수 비교

지금까지 출력층에서 사용하는 항등 함수와 소프트맥스 함수를 살펴보았다. 이제는 예시에 직접 적용해보면서 각 함수들의 결과들을 비교해보고자 한다. 예시로 사용할 배열은 은닉층 활성화 함수들 비교했던 x를 그대로 사용하기로 한다.

1	Julia> x = [-1 -2 -3;0 3 7]

먼저 항등 함수부터 확인해보자.

Julia> identity_function(x)
2×3 Array{Int64,2}:
 -1  -2  -3
  0   3   7

입력값을 그대로 반환하는 것을 알 수 있다. 그 다음으로는 소프트맥스 함수를 적용해보자.

Julia> softmax(x)
2×3 Array{Float64,2}:
 0.000328971  0.000121022  4.45214e-5
 0.000894237  0.0179612    0.98065

$0$과 $1$ 사이의 값들로 변환되어 출력하는 것을 확인할 수 있다. 여기서 소프트맥스가 제대로 구현되었는지 확인하려면 모든 요소들을 더해서 $1$이 나오면 된다.

1 2	Julia> sum(softmax(x)) 1.0

요소들의 합이 $1$임을 확인할 수 있다.