3. 손실 함수

해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.

손실 함수란

신경망을 사용하기 위해서는 그 전에 학습을 통해 올바른 기준을 생성해주어야 한다. 이런 과정을 ‘신경망 학습’이라고 한다. 신경망 학습에서는 훈련 데이터를 사용하며, 이를 통해 신경망이 실전 문제에서도 적절하게 접근할 수 있도록 하는 가중치를 찾는다. 그렇다면 신경망 학습이 잘 이루어지고 있는지 어떻게 알 수 있을까? 여기서 ‘손실 함수’가 사용된다. 손실 함수(loss function)는 신경망을 평가하는 평가지표로서 사용되며, 오답률을 나타낸다. 즉, 손실 함수의 값이 0에 가까울수록 좋은 신경망이라는 것이다. 보통 손실 함수는 정답과 신경망이 도출한 출력 값을 비교하여 나타낸다.

일반적으로 사용하는 손실 함수로는 평균 제곱 오차와 교차 엔트로피 오차가 있다.

평균 제곱 오차

‘평균 제곱 오차(Mean Squared Error, MSE)’는 출력 값에서 정답을 뺀 결과를 제곱하여 더한 값들을 비교한다. 수식은 아래와 같다.

$E=\frac{1}{n}\sum_{i=1}^n (y_i-t_i)^2$

위의 수식에서 $y_i$는 출력 값, $t_i$는 정답이며 $n$은 원소의 개수이다. 출력 값에서 정답을 뺀 오차를 제곱하여 $n$으로 나눠줌으로써 평균을 손실 함수의 값으로 제공한다.

위의 수식을 코드로 구현하면 다음과 같다.

function mean_squared_error(y,t)
    error = (y-t).^2
    return sum(error) / length(y)
end

좀 더 정확한 이해를 위해 예시를 확인해보자.

1
2
3

Julia> t = [0 0 1 0 0 0 0 0 0 0] # 정답 레이블
Julia> y1 = [0.1 0.05 0.6 0.0 0.05 0.1 0.0 0.1 0.0 0.0] # 출력 값 with 정답
Julia> y2 = [0.1 0.05 0.1 0.0 0.05 0.1 0.0 0.6 0.0 0.0] # 출력 값 with 오답

먼저 정답 배열인 t와 출력 배열인 y1, y2를 세팅해준다. 해당 예시는 예측값이며 y1, y2는 소프트맥스 함수의 결과이다. y1은 정답을 맞춘 출력 값이고, y2는 오답인 출력 값이다. 그렇다면 출력 값 y1, y2을 사용하여 오차 값을 구해보자.

Julia> mean_squared_error(y1,t)
0.019500000000000007

Julia> mean_squared_error(y2,t)
0.11949999999999998

정답에 높은 확률을 할당한 결과 값 y1은 오차로 $0.0195$이며, 오답에 높은 확률을 할당한 결과 값 y2는 오차로 $0.1194$가 나왔다. 즉, y1이 y2보다 더 잘 예측했음을 알 수 있다.

교차 엔트로피 오차

‘교차 엔트로피 오차(Cross Entropy Error, CEE)’는 자연로그를 이용한 함수이다. 수식은 아래와 같다.

$E=-\sum_{i=1}^n (t_i\times\ln y_i)$

위의 식은 정답 레이블 t와 출력 값을 곱한다. 여기서 정답 레이블은 오답과 정답을 0과 1로 표현한 것이기 때문에 오답인 경우는 출력 값과 0이 곱해진다. 즉, 정답 위치와 같은 출력 값만 자연로그 값이 제공되며 나머지는 $0$으로 반환된다. 위의 수식에서는 2가지의 의문이 제기될 수 있다.

첫 번째 의문은 “하나의 값을 제외한 나머지가 0임에도 불구하고 왜 $\sum$(시그마)를 사용하는가?”이다. 그 이유는 배열을 하나의 값으로 반환하기 위해서이다. $t_i*\ln y_i$식을 계산하면 아래와 같은 결과가 도출된다.

Julia> delta = 1e-7
Julia> -log.(y1.+ delta).* t
1×10 Array{Float64,2}:
 0.0  0.0  0.510825  0.0  0.0  0.0  0.0  0.0  0.0  0.0

이 결과에서 0이 아닌 값만 도출하는 것은 쉬워보이지만, 정답 레이블에서 1의 위치가 계속 변하기 때문에 기술적으로 복잡하다. 그렇기 때문에 하나의 값을 도출하기 위해서 모두 더한 것이다. 한 값을 제외하고 전부 0이기 때문에 이는 배열에서 스칼라로 변한 것뿐 수학적인 문제는 없다.

두 번째 의문은 “왜 자연로그를 이용하는가?”이다. 먼저 자연로그 그래프를 살펴보자.

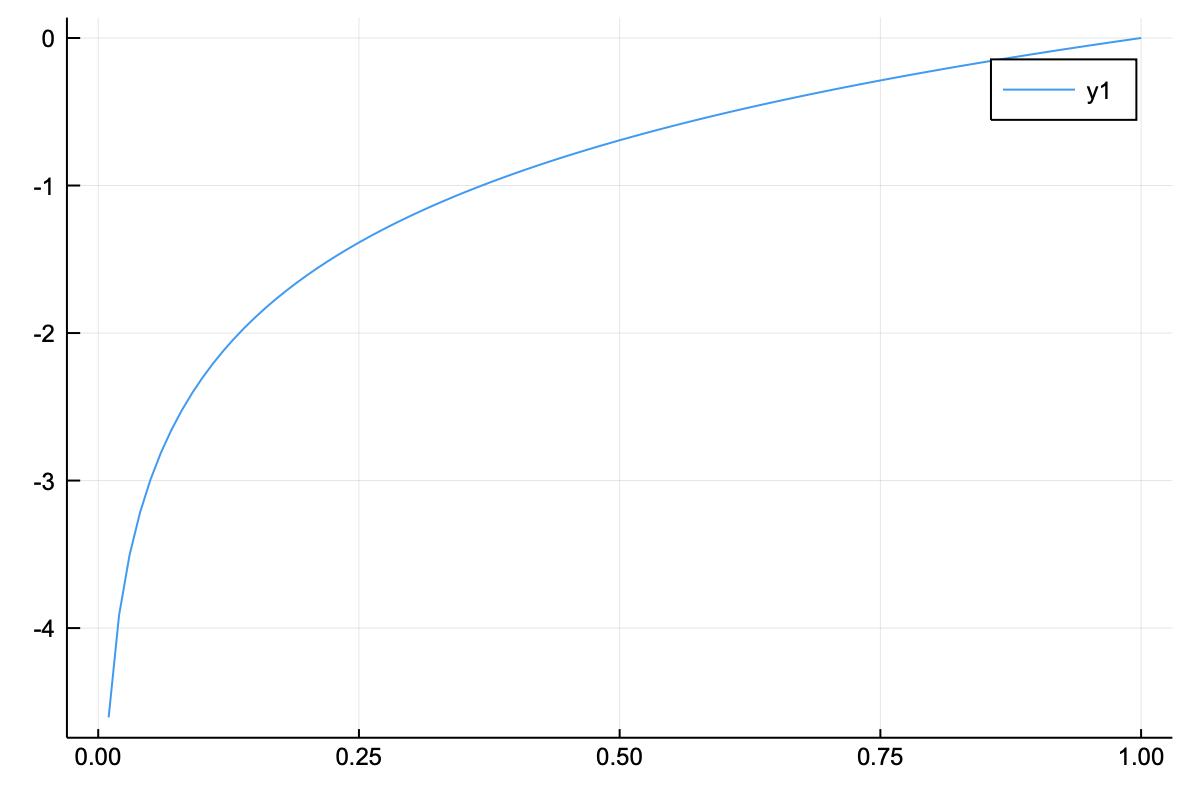
위의 그래프에서는 $x$축이 1일 때 $y$축이 0이며, $x$축이 1 미만일 때에는 $-e$에 가까운 값으로 향한다. 즉, 0부터 1 사이의 수들은 전부 음수로 반환되는 것이다. 이런 원리를 이용하여 정답레이블 1에 위치한 소프트맥스 함수의 확률 값이 1에 가까울수록 작은 수로 변환되며, 이를 통해서 판단지표의 역할을 하는 것이다. 음수로 나오는 결과를 양수로 변환하기 위해서 $log$ 앞에 $-$ 를 곱한다.

해당 수식을 코드로 구현하면 다음과 같다.

function cross_entropy_error(y, t)
    delta = 1e-7
    return -sum(log.(y.+ delta).* t)
end

위의 정의에서 delta 또한 기술적인 이유로 포함되었다. 그래프에서도 확인할 수 있듯이 자연로그는 $x$축이 0인 경우의 $y$값이 마이너스 무한대이다. 따라서 $log_e 0$은 -inf이기 때문에 계산 오류가 바로 발생한다. 이를 막기 위해 아주 작은 값인 $1e-7$을 더해주는 것이다. $1e-7$은 지수 표기법으로 $0.0000001$을 의미한다.

지금부터 예시에 교차 엔트로피 오차를 적용해보자.

1
2
3

Julia> t = [0 0 1 0 0 0 0 0 0 0] # 정답 레이블
Julia> y1 = [0.1 0.05 0.6 0.0 0.05 0.1 0.0 0.1 0.0 0.0] # 출력 값 with 정답
Julia> y2 = [0.1 0.05 0.1 0.0 0.05 0.1 0.0 0.6 0.0 0.0] # 출력 값 with 오답

예시 데이터셋은 평균 제곱 오차에서 사용했던 것을 그대로 사용할 것이다.

Julia> cross_entropy_error(y1,t)
0.510825457099338

Julia> cross_entropy_error(y2,t)
2.302584092994546

위의 결과를 보면 잘 예측한 y1이 잘못 예측한 y2보다 더 작은 것을 확인할 수 있다. 이처럼 손실 함수는 오차를 계산하여 오차율을 나타내며, 값이 0에 가까울수록 오차가 없다고 판단한다. 즉, 손실 함수의 값이 0에 가까울수록 해당 신경망은 잘 학습되었다고 평가되는 것이다.