Linear Algebra (1)

글을 시작하기에 앞서 해당 글은 Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong의 저서인 mathematics for machine learning을 바탕으로 요약 및 정리한 글임을 알려드립니다.

---

벡터(vector)란

일반적으로 동일한 종류의 두 객체를 합하거나 스칼라와 곱해서 같은 종류의 다른 객체를 생성할 수 있다면 이를 벡터라고 한다. 좀 더 추상적인 수학적 관점에서 벡터를 정의한다면, 앞의 두 조건을 만족하는 모든 객체들이 벡터로 간주된다.

• ‘기하학에서의 벡터(Geometric vector)’도 합과 스칼라 곱이 가능하기 때문에 벡터이다.

• ‘다항식(Polynomials)’도 서로 더하거나 스칼라를 곱할 수 있기에 벡터 중 하나이다.

• ‘오디오 신호(Audio signals)’도 숫자의 열거이기에 신호끼리 서로 더하거나 연산할 수 있다. 따라서 벡터 중 하나이다.

• $\mathbb{R}^n$(실수 집합)의 요소도 벡터이다. 이 책에서 가장 중요한 벡터 개념이기에 예시로 설명하고자 한다.

  $$a= \begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix} \in \mathbb{R}^3$$

위의 예시 $a$는 삼항이고, 따라서 $\mathbb{R}^3$에 속한다. 이 벡터를 다른 벡터 $b$와 더해도 그 결과값이 $\mathbb{R}^3$에 속하며, 스칼라 $\lambda$와 곱해도 그 결과값이 $\mathbb{R}^3$에 속한다. 따라서 이 또한 벡터이다. $\mathbb{R}^n$의 요소들을 벡터로 전제하면 배열을 사용하여 벡터 연산이 가능하기에 훨씬 편리하다. 선형대수의 알고리즘 대부분이 $\mathbb{R}^n$로 공식화되기 때문에 우리는 $\mathbb{R}^n$안에서의 벡터에 집중할 것이다.

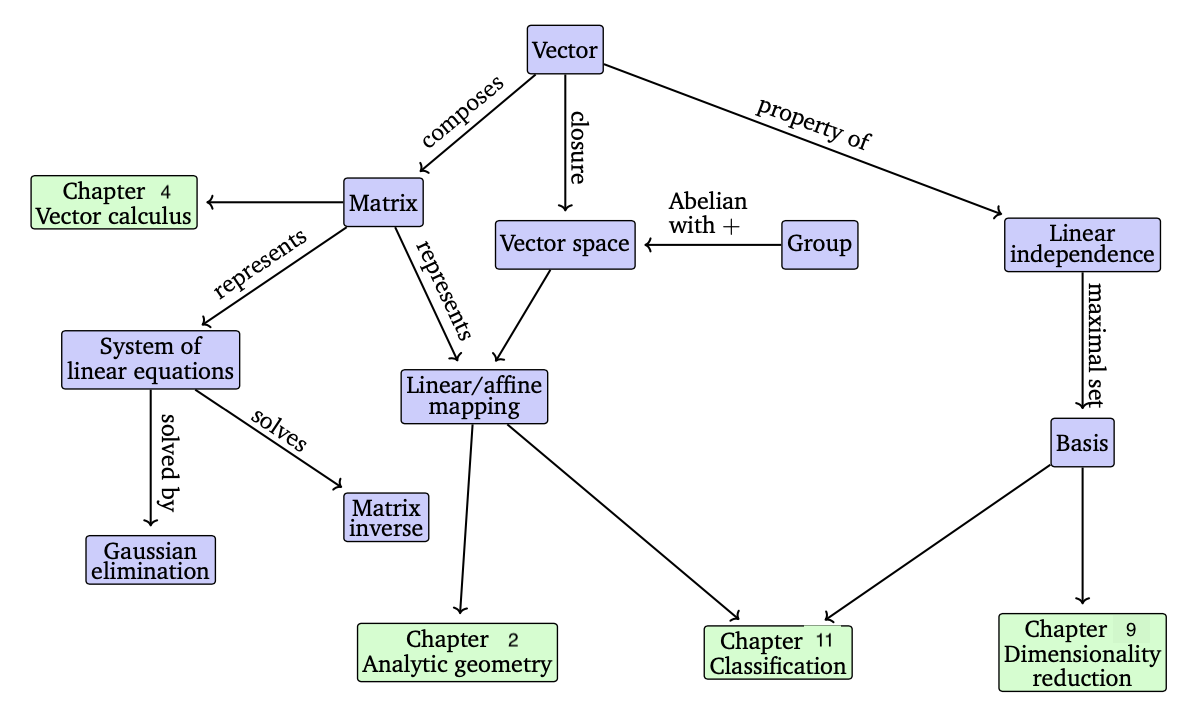
수학의 주요 아이디어 중 하나는 폐포(closure)이다. 폐포의 의미는 주어진 작업에서 발생할 수 있는 모든 것들을 나타내는 것이다. 즉, 어떤 연산를 통해 발생할 수 있는 모든 결과들을 보여주는 것이다. 이를 벡터 개념에서 적용한다면 의미는 다음과 같다. 작은 벡터들을 더하고 크기를 조정할 때 어떤 벡터가 만들어지는가? 이 질문에 대한 답이 ‘벡터 공간’이다. 벡터 공간에 대해서는 이후 자세히 다룰 것이다. 아래의 그림은 이번 장에서 보여주는 개념들을 요약한 도식이다.

연립 선형방정식 (Systems of Linear Equations)

연립 선형방정식은 선형대수의 중요한 핵심 파트 중 하나이다. 연립 선형방정식에 대한 설명은 예시를 살펴보면서 진행하자.

$$4x_1 + 4x_2 = 5$$ $$2x_1 - 4x_2 = 1$$

위의 두 수식은 두 개의 변수로 구성된 연립 선형방정식이다. 위의 두 식을 모두 만족하는 $x_1$의 값과 $x_2$의 값을 구하려고 한다. 이를 그래프로 나타내면 아래와 같다.

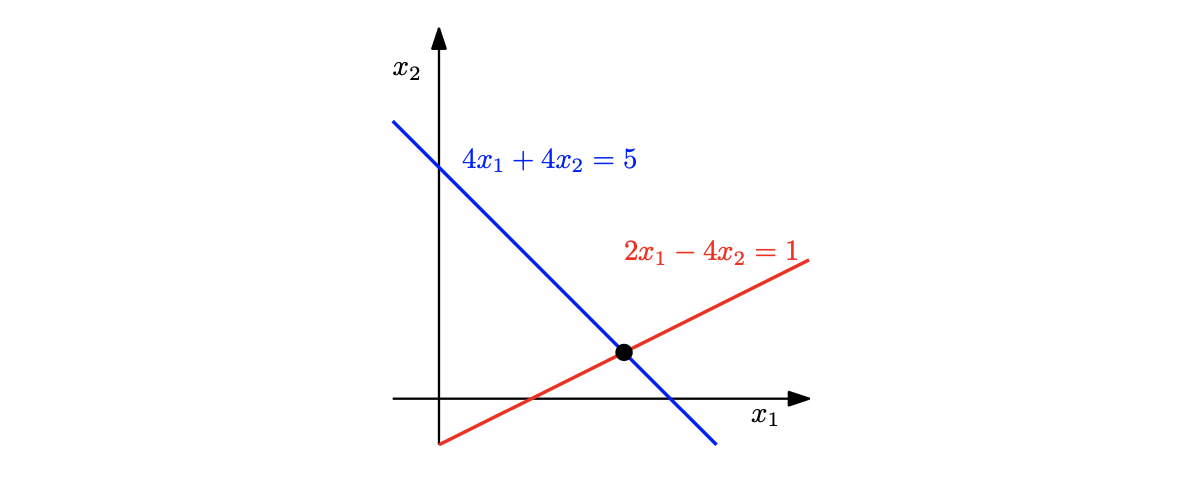
두 수식을 모두 만족하는 값은 위 그래프의 ‘검은 점’이다. 위의 수식을 정리해보면 검은 점의 좌표는 $(1, \frac{1}{4})$인 것을 알 수 있다.

변수가 2개일 때는 위의 예시와 같이 2차원 그래프를 그린 후 겹쳐지는 점을 구하면 된다. 그렇다면 변수가 세 개인 경우에는 어떻게 해야 할까? 변수의 개수와 동일하게 차원이 증가하기 때문에 3차원 그래프로 나타낼 수 있다. 또한 변수가 세 개인 경우에는 겹쳐지는 지점으로 평면(plane)이 등장한다.

연립 선형방정식을 좀 더 일반화하면, 아래와 같은 결론을 도출할 수 있다.

• 1단계: 변수 n개인 연립 선형방정식

$$a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1\\ \vdots\\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n = b_m$$

• 2단계: 벡터인 변수의 계수(coefficient)를 행렬(matrix)로 변경하기

$$x_1\begin{bmatrix} a_{11}\\ \vdots\\ a_{m1} \end{bmatrix} + x_2\begin{bmatrix} a_{12}\\ \vdots\\ a_{m2} \end{bmatrix} + \cdots + x_n\begin{bmatrix} a_{1n}\\ \vdots\\ a_{mn} \end{bmatrix} = \begin{bmatrix} b_{1}\\ \vdots\\ b_{m} \end{bmatrix}$$

• 3단계: 변수도 행렬(matrix)로 변경하기 ($Ax=b$)

$$\begin{bmatrix} a_{11} & \cdots & a_{1n}\\ \vdots & & \vdots\\ a_{m1} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} b_{1}\\ \vdots\\ b_{m} \end{bmatrix}$$

행렬 (Matrices)

행렬은 선형대수에서 가장 중요한 원리이다. 연립 선형방정식을 간단하게 나타내기 위해 사용하기도 하며, 이후 자세히 다룰 ‘선형 변환 (linear mapping)’에서도 사용된다. 행렬에 대한 흥미로운 주제를 다루기 전에 행렬이 무엇인지 간단히 살펴보자.

$m, n \in \mathbb N$(자연수)인 행렬 A는 행이 $m$이고 열이 $n$인 튜플(tuple)이며, $i=1\cdots m$이고 $j=1 \cdots n$인 $a_{ij}$를 요소로 가진다. 해당 정의를 수식으로 표현하면 다음과 같다.

$$A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} , a_{ij} \in \mathbb R$$

행렬의 각각 행과 열은 행벡터 또는 열벡터이며, $\mathbb R^{m\times n}$은 모든 $m \times n$행렬을 포함한다. 위의 예시인 $A$ 또한 $m \times n$에 포함된다. 행렬 $A$는 긴 벡터형태인 $a$로 나타낼 수 있으며, $a \in \mathbb R^{mn}$이다. 예로 행렬 $A$가 $\mathbb R^{4\times 2}$에 포함된다면, $a$는 $\mathbb R^8$에 포함된다.

행렬의 덧셈과 곱셈

행렬 $A$와 $B$ 모두가 $\mathbb R^{m \times n}$에 속한다면, 두 행렬은 더할 수 있다.

$$A+B:=\begin{bmatrix} a_{11}+b_{11} & \cdots & a_{1n}+b_{1n}\\ \vdots & & \vdots\\ a_{m1}+b_{m1} & \cdots & a_{mn}+b_{mn} \end{bmatrix} \in \mathbb R^{m \times n}$$

행렬 $A$가 $\mathbb R^{m \times n}$에 속하고, 행렬 $B$가 $\mathbb R^{n \times k}$에 속한다면, $C=AB\in\mathbb R^{n \times k}$이다.

$$c_{ij}=\sum_{l=1}^n a_{il}b_{lj} \quad\quad i=1 \cdots m,\quad j= 1 \cdots k$$

행렬 $A$와 $B$의 곱인 $C$의 요소는 $A$의 행과 $B$의 열의 곱과 같다. 행렬의 행과 열을 곱하는 것을 ‘내적(dot product)’이라고 부르며, 자세한 내용은 2장에서 다룰 것이다. 내적은 기호 “ $\cdot$ “로 나타낸다.

다시 한번 강조하지만 두 행렬의 곱은 이웃하는 차원이 동일해야 가능하다. $m \times n$인 행렬 $A$는 $n \times k$인 행렬 $B$와 곱할 수 있으며, 그 결과는 $m \times k$행렬이다. 즉, $AB$는 가능하다. 하지만 $BA$의 경우는 이웃하는 차원이 동일하지 않기 때문에 곱할 수 없다.

하지만 프로그래밍에서는 지금까지 봤던 곱의 원리와는 다르게 행렬의 요소끼리 곱셈을 하는 ‘아다마르 곱(Hadamard product)’도 가능하다. 아다마르 곱은 같은 $m \times n$크기의 두 행렬이 같은 위치에 있는 요소끼리 곱해지는 것이며, 행렬 덧셈의 원리와 같다.

‘항등 행렬(Identity Matrix)’은 $n \times n$ 행렬로 $\mathbb R^{n \times n}$에 속한다. 항등 행렬의 요소는 행과 열의 위치가 같은 주대각선(main diagonal)만 1이고, 나머지는 0이다. 도식화하면 다음과 같다.

$$I_n=\begin{bmatrix} 1 & 0 & \cdots & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & 1 & \cdots &0\\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & 0 & \cdots &1 \end{bmatrix} \in \mathbb R^{n \times n}$$

지금까지 행렬의 덧셈과 곱셈에 대해 살펴보았다. 행렬은 다음과 같은 특징을 가진다.

• 결합법칙(Associativity)

$A \in \mathbb R^{m \times n},\quad B \in \mathbb R^{n \times q},\quad C \in \mathbb R^{q \times p} \ :\ (AB)C = A(BC)$

• 분배법칙(Distributivity)

$A \in \mathbb R^{m \times n},\quad B, C \in \mathbb R^{n \times q} \ :\ A(B+C) = AB + AC$

• 항등행렬과의 곱

$A \in \mathbb R^{m \times n} \ :\ I_mA = AI_n = A$

역행렬과 전치행렬

행렬 $A \in \mathbb R^{n \times n}$와 행렬 $B \in \mathbb R^{n \times n}$가 있다. 만약 행렬 $A, B$에 대해서 $AB = I_n = BA$가 성립한다면, $B$는 $A$의 ‘역행렬(inverse matrix)’이다. $A$에 대한 역행렬의 기호는 $A^{-1}$이다.

모든 행렬이 역행렬을 가진 것은 아니다. 역행렬이 존재하는 경우 해당 행렬을 가역 행렬 또는 비특이 행렬이라고 하며, 존재하지 않는 경우 비가역 행렬이라고 한다.

$$A:=\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{bmatrix} \in \mathbb R^{2 \times 2}$$

행렬 $A$를 $2 \times 2$행렬로 정의한다.

$$B:=\begin{bmatrix} a_{22} & -a_{12}\\ -a_{21} & a_{11}\\ \end{bmatrix} \in \mathbb R^{2 \times 2}$$

행렬 $A$와 곱해서 항등 행렬이 나올 수 있는 행렬 $B$를 정의한다.

$$AB=\begin{bmatrix} a_{11}a_{22}-a_{12}a_{21} & 0\\ 0 & a_{11}a_{22}-a_{12}a_{21}\\ \end{bmatrix} = (a_{11}a_{22}-a_{12}a_{21})I$$

두 행렬을 곱한 후, 항등 행렬 기준으로 식을 정리한다.

$$A^{-1}= \frac{1}{a_{11}a_{22}-a_{12}a_{21}} \begin{bmatrix} a_{22} & -a_{12}\\ -a_{21} & a_{11}\\ \end{bmatrix}$$

그 결과 행렬 $A$의 역행렬을 구할 수 있다.

정리하면 다음과 같다. 행렬 $A$와 곱해서 항등 행렬 $I$가 나온다면 그 행렬은 역행렬 $A^{-1}$이다.

일반적으로 전치행렬 $A^T$은 행렬 $A$의 행과 열이 바뀐다. 즉, 행렬 $A$가 $m \times n$이라면 전치행렬인 $A^T$는 $n \times m$인 것이다. 전치행렬은 주대각선(main diagonal)을 기준으로 뒤집힌 행렬을 말한다.

$$A=\begin{bmatrix} \mathbf{a_{11}} & a_{12}\\ a_{21} & \mathbf{a_{22}}\\ \end{bmatrix} \quad A^T=\begin{bmatrix} \mathbf{a_{11}} & a_{21}\\ a_{12} & \mathbf{a_{22}}\\ \end{bmatrix}$$

지금까지 역행렬과 전치행렬의 정의에 대해서 살펴보았다. 역행렬과 전치행렬은 아래와 같은 특징을 가진다.

1. 역행렬

• $AA^{-1} = I = A^{-1}A$
• $(AB)^{-1} = A^{-1}B^{-1}$
• $(A+B)^{-1} \ne A^{-1} + B^{-1}$

1. 전치행렬

• $(A^T)^T = A$
• $(A+B)^T = A^T + B^T$
• $(AB)^T = B^TA^T$

역행렬은 $n \times n$ 형태의 가역 행렬일 때만 존재한다. 따라서 행렬 $A$가 가역 행렬이고 역행렬 $A^{-1}$가 존재한다면, 아래와 같은 식도 성립한다.

$(A^{-1})^T = (A^{T})^-1 =: A^{-T}$

행렬과 스칼라의 곱

행렬 $A$에 스칼라 $\lambda$를 곱해보자. 여기서 행렬 $A$는 $\mathbb R^{m \times n}$에 속하고, 스칼라 $\lambda$는 실수 $\mathbb R$에 속한다. 스칼라 $\lambda$는 행렬 $A$의 요소들에 각각 곱해진다. 이를 기호로 나타내면 $\lambda A=K$, $K{ij} = \lambda a{ij}$ 이다. 스칼라 $\lambda, \psi$을 행렬과 곱할 때, 다음과 같은 특징을 가진다.

• 결합법칙(Associativity)

$(\lambda\psi)C = \lambda(\psi C),\quad C \in \mathbb R^{m \times n}$

$\lambda(BC) = (\lambda B)C = B(\lambda C)= (BC)\lambda, \quad B \in \mathbb R^{m \times n}, C \in \mathbb R^{n \times k}$

$(\lambda C)^T = C^T\lambda^T = C^T\lambda = \lambda C^T$

• 분배법칙(Distributivity)

$(\lambda + \psi)C = \lambda C + \psi C,\quad C \in \mathbb R^{m \times n}$

$\lambda(B + C)=\lambda B + \lambda C,\quad B,C \in \mathbb R^{m \times n}$