12. 인공신경망 최적화 - 가중치 초기값

해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.

가중치 초기값이란

이전 글에서 우리는 최적화 방법 중 하나인 옵티마이저에 대해서 살펴보았다. 이번 글에서는 두 번째 최적화 방법인 ‘가중치 초기값 설정 방법’에 대해서 공부할 것이다. 모든 신경망 구조는 초기에 매개 변수를 랜덤으로 설정한다. 매개 변수를 생성하는 코드를 다시 확인해보자.

function making_network(input_size, hidden_size, output_size, weight_init_std =0.01)
    params["W1"] = weight_init_std * randn(Float64, input_size, hidden_size)
    params["b1"] = zeros(Float32, 1, hidden_size)
    params["W2"] = weight_init_std * randn(Float64, hidden_size, output_size)
    params["b2"] = zeros(Float32, 1, output_size)
    return(params)
end

위 코드에서 우리는 상수 weight_init_std가 W에 곱해지는 것을 확인할 수 있다. 이는 정규분포를 기반으로 랜덤값을 생성한 W에 0.01을 곱해 W를 더 작게 만든 것이다. W를 작게 만드는 이유는 ‘기울기 소실(Gradoent Vanishing)’을 방지하기 위해서이다.

Note
기울기 소실(Gradoent Vanishing)이란?
깊은 신경망을 학습하다보면 기울기의 값이 점점 작아지면서 아예 0이 되는 상황을 말한다. 이는 신경망 자체의 문제라기보다는 활성화 함수에 연계된 문제이다. 예를 들어 시그모이드 함수의 경우, 0-1사이의 범위에서 결과값들을 도출하는데, 그 결과값들이 0과 1에 가까워질수록 기울기가 0으로 수렴한다. 즉, 기울기가 사라지는 것이다. 이런 문제는 활성화 함수에 맞춰 초기값 설정을 잘하면 어느정도 방지할 수 있다.

std

std는 “standard deviation”의 약자로 표준편차를 의미하며, 지금까지 우리가 사용했던 방식이다. 식은 다음과 같다.

$W := 0.01 \times W$

std는 가중치 초기값 설정에서 정규분포 기반의 랜덤값을 생성한 후, 0.01을 곱한다. 이런 방식은 가중치 초기값을 0과 1사이의 값으로 설정하면서 얕은 신경망의 기울기 소실 문제는 막아준다. 하지만 깊은 신경망을 학습시키는 경우에는 각 층을 지날수록 output값이 0.5에 수렴하는 문제가 발생한다. 이는 다양한 범위를 가진데이터의 표현력을 제한하는 결과를 초래한다. 따라서 깊은 신경망에서는 다른 초기값을 사용하는 것이 데이터의 특징을 잘 학습할 수 있다. 다른 초기값으로는 시그모이드 함수와 같은 S자 함수에 사용되는 “Xavier” 초기값과 ReLU와 같은 함수에 사용되는 “He” 초기값이 있다.

Xavier

Xavier 초기값은 처음 이를 제안한 ‘사비에르 글로로트(Xavier Glorot)’의 이름을 가져왔으며, 수식은 다음과 같다.

$W := \sqrt\frac{1}{n} \times W$

위 수식에서 n은 앞 계층의 노드 갯수이다. 예를 들어, 입력값이 $1 \times 784$개이고, 첫 번째 가중치의 초기값을 구하려고 한다. 그렇다면 n은 $784$가 될 것이다. 또한 앞의 노드가 $1 \times 50$이라고 한다면, n은 $50$이 된다.

Xavier 초기값은 가중치에 이전 노드 갯수와 반비례 관계를 생성하여 출력값들이 정규분포 형태를 유지하도록 해준다. 즉, 이전 노드가 많았다면 가중치의 값은 더 작아지며, 이전 노드가 적었다면 가중치의 값을 크게하여 초기의 정규분포 형태를 계속 유지해주는 것이다. 하지만 이 방법은 S자 함수에 적합하며, ReLU와 같은 비선형 함수에는 적합하지 않다. 그 이유는 위 방법이 대칭 구조에 적합하기 때문이다. ReLU의 경우 음수는 모두 0으로 처리되기 때문에 이전 대부분의 노드가 음수라면 출력값이 0쪽으로 치우친다. 따라서 ReLU와 같은 비선형 함수는 그에 맞는 초기값 설정이 필요하다.

He

He 초기값은 처음 이를 제안한 ‘카이밍 히(kaiming He)’의 이름을 가져왔으며, 수식은 다음과 같다. 참고로 He 초기값에서 쓰인 n 또한 위에서 설명한 바와 같다.

$W := \sqrt\frac{2}{n} \times W$

수식을 살펴보면 $\frac{2}{n}$에서 2를 제외하고는 Xavier 초기값과 동일한 것을 알 수 있다. 실제로 He 초기값은 ReLU의 특수성을 반영하기 위해 Xavier 초기값을 변형한 결과이다. ReLU 함수는 음수를 전부 0으로 처리함으로써 그 결과값의 그래프가 자연스레 0으로 편향될 수밖에 없다. 따라서 기존 표준편차에 2를 곱해 차이를 극대화해줌으로써 출력값의 편향을 억제한다.

가중치 초기값 설정하기

이제는 우리에게 3가지의 가중치의 초기값이 있다. 이를 편하게 사용하기 위해서 매개 변수를 생성하는 코드를 일반화하려고 한다. 먼저 완성된 함수는 아래와 같다.

function making_network(W, b, weight_size, output_shape, weight_init)

    params = Dict()

    if weight_init == "std"
        for i in (1:length(W))
            params[W[i]] = 0.01 * randn(Float64, weight_size[i])
            params[b[i]] = zeros(Float64,1, weight_size[i][end])
        end
        return(params)

    elseif weight_init == "Xavier"
        for i in (1:length(W))
            params[W[i]] = ((1.0 / prod(output_shape[i]))^(1/2)) * randn(Float64, weight_size[i])
            params[b[i]] = zeros(Float64,1, weight_size[i][end])
        end
        return(params)

    elseif weight_init == "He"
        for i in (1:length(W))
            params[W[i]] = ((2.0 /prod(output_shape[i]))^(1/2)) * randn(Float64, weight_size[i])
            params[b[i]] = zeros(Float64,1, weight_size[i][end])
        end
        return(params)
    end
    return(params)
end

이제 사용법을 확인해보자. making_network()은 입력 변수로 W, b, weight_size, output_shape, weight_init 을 받는다. 하나씩 살펴보자.

(Summary)

W: 신경망에 필요한 가중치 ( 배열로 구성, ex. 2층 신경망 = [“W1”, “W2”] )
b: 신경망에 필요한 편향 ( 배열로 구성, ex. 2층 신경망 = [“b1”, “b2”] )
weight_size: 은닉층의 사이즈 ( 배열로 구성 )
output_shape: 층마다 결과값으로 도출되는 사이즈 ( 배열로 구성 )
weight_init: 초기값 설정 ( “std”, “Xavier”, “He” 중 선택 )

만약 하나의 신경망을 구성하고 학습시키려고 한다. 그럼 첫 번째로 해야할 일은 신경망 구조를 설정하는 것이다. 여기서는 2층 신경망을 만들기로 했다고 가정하자. 그러면 필요한 가중치와 편향은 2개씩이다. 이를 배열로 정의하여 설정한다.

1 2	W = ["W1", "W2"] b = ["b1", "b2"]

그 다음 설정해야 하는 것은 은닉층의 개수이다. 보통 신경망에 사용할 데이터에 따라서 입력값과 출력값은 결정된다. 결국 신경망 구조에서 우리가 결정하는 부분은 은닉층에 관해서이다. MNIST데이터를 사용한다고 가정하고 아래의 수식을 확인해보자.

$Input(1 \times 784) \times Hidden(784 \times ?) \times Output(? \times 10)$

위 수식은 MNIST데이터 기반의 2층 신경망 구조를 나타낸 것이다. 가중치는 $Input$과 $Hidden$ 사이에 1개, $Hidden$과 $Output$사이에 1개가 필요하다. 따라서 총 두 개의 가중치를 변수 weight_size 자리에 입력해줄 것이다. weight_size는 가중치 크기의 튜플을 배열의 요소로 저장한다. 이제 2층 신경망에 맞게 weight_size를 설정해보자. 해당 예시에서는 ?을 50으로 설정할 것이다. output_shape은 각 층의 결과값 크기를 배열의 요소로 저장한다. weight_size에 따라서 다음 층의 결과값 크기가 결정된다.

1 2	weight_size = [(784, 50), (50,10)] output_shape = [(1,784),(1,50)]

이제 마지막으로 우리가 설정할 수 있는 입력 변수는 weight_init가 있다. 지금 생성한 2층 신경망의 활성화 함수를 ReLU로 설정할 것이기 때문에 가중치 초기값으로 “He”를 선택할 것이다. 이제 매개 변수를 생성할 준비가 완료되었다. 아래의 코드를 입력하면 2층 신경망에 필요한 매개 변수가 생성된다.

1	params = making_network(W, b, weight_size, output_shape, "He")

making_network()는 매개 변수들의 초기값을 담은 딕셔너리를 도출한다. 이를 네트워크로 사용하고 싶은 이름에 할당하자. 여기서 할당되는 딕셔너리는 학습 후에 해당 신경망의 매개 변수들을 담고 있는 ‘핵심’이 될 것이다. 새롭게 튜닝된 making_network()는 어떤 구조의 신경망이라도 가중치와 편향 초기값을 생성하기에 이전의 버전보다 훨씬 사용하기 편리하다.

가중치 초기값 별 결과

위에서 설명한 making_network()을 통해서 각 초기값들을 신경망에 적용해보고자 한다. 이번에 학습시킬 신경망의 구조는 다음과 같다.

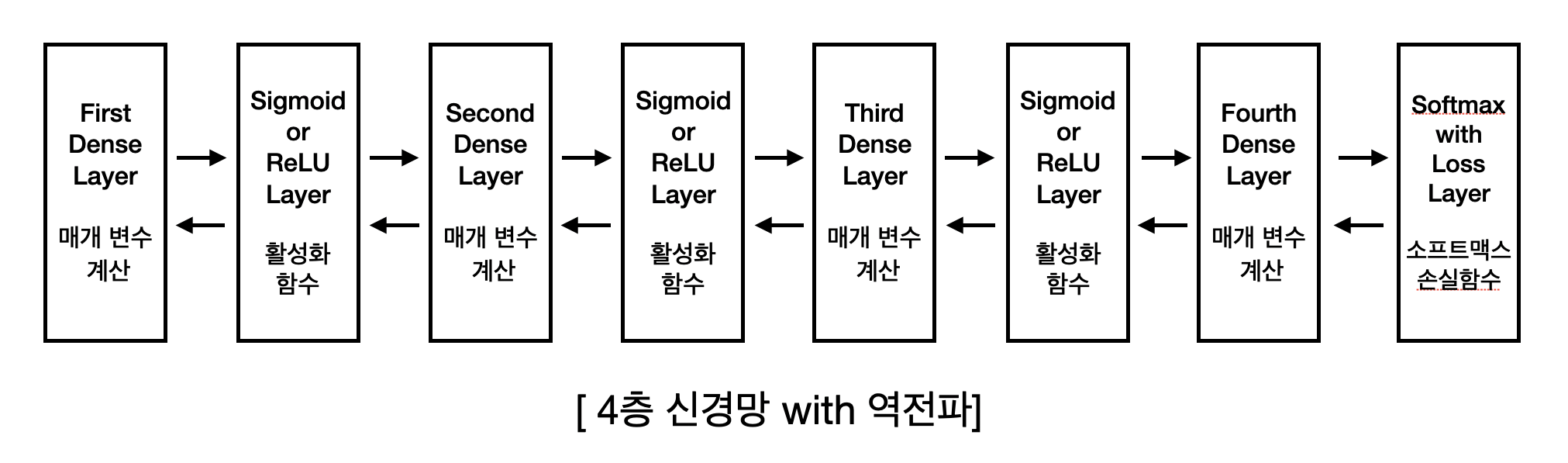
4층 구조
MNIST 데이터셋
역전파 알고리즘
optimizer: Adam
배치데이터(100단위) 사용
3에폭 훈련 예정

He초기값과 Xavier 초기값의 정확한 측정을 위해 활성화 함수는 “ReLU”와 “Sigmoid” 두 가지 버전으로 나누어 학습할 것이다.

먼저 활성화 함수로 Sigmoid를 사용한 학습 결과를 확인해보자.

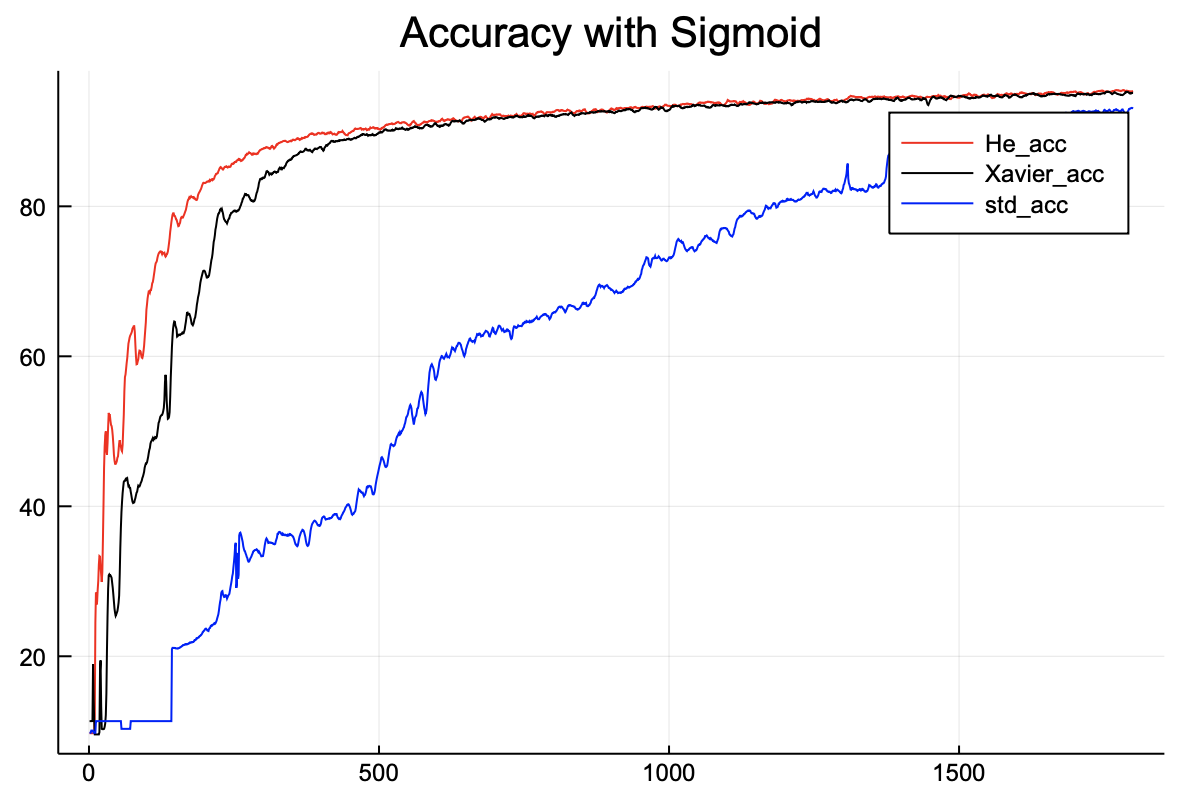
위 그래프는 sigmoid 기반 4층 신경망의 정확도를 각 가중치 초기값 별로 나타낸 것이다. 확실히 std 초기값을 사용한 것보다 Xavier, He초기값을 사용하여 학습한 것이 더 높은 정확도를 도출한다.

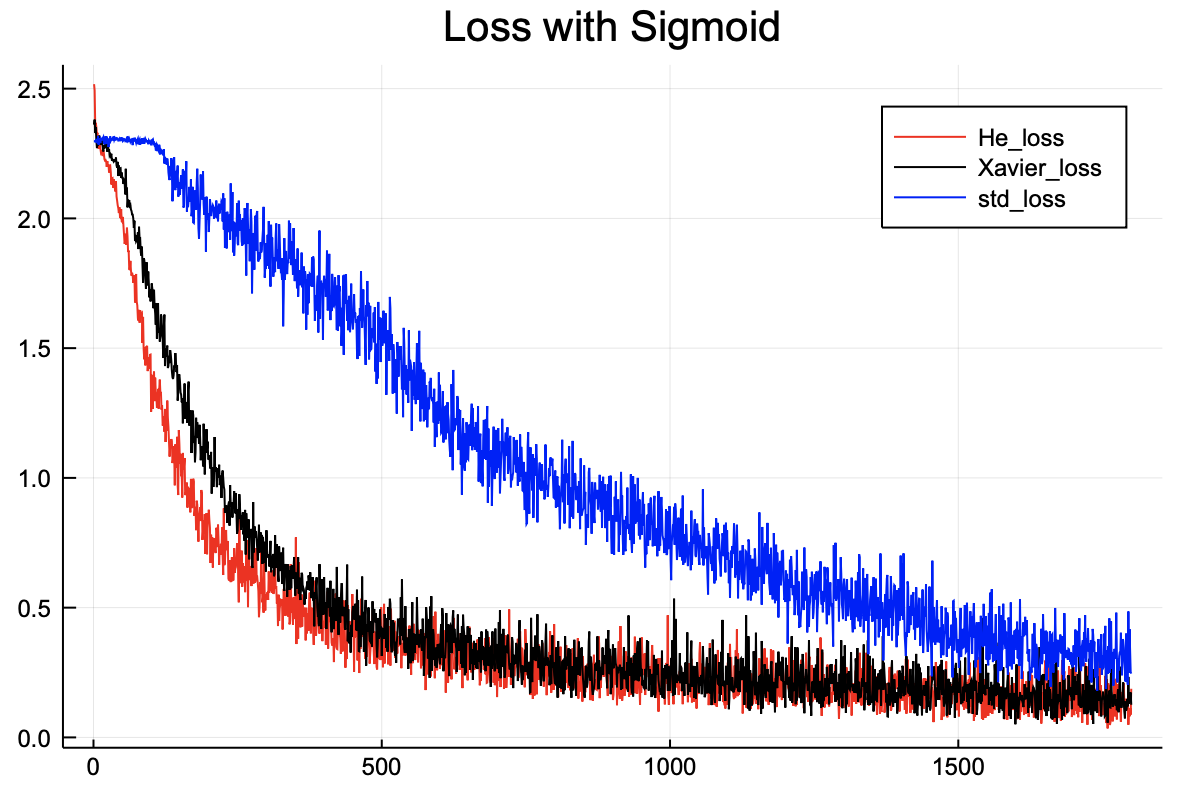
손실함수를 비교해보면 차이가 더 명확히 보인다. 또한 Xavier, He초기값은 비슷한 결과를 도출한다. 시그모이드와 같은 S자 함수에서는 Xavier와 He 둘다 어느정도 효율을 높여주는 것 같다.

그 다음으로 살펴볼 것은 활성화 함수로 ReLU를 사용한 학습 결과이다. ReLU는 특이한 형태의 비선형 함수이기 때문에 치우침 현상을 막기 위해서는 He 초기값이 더 좋다.

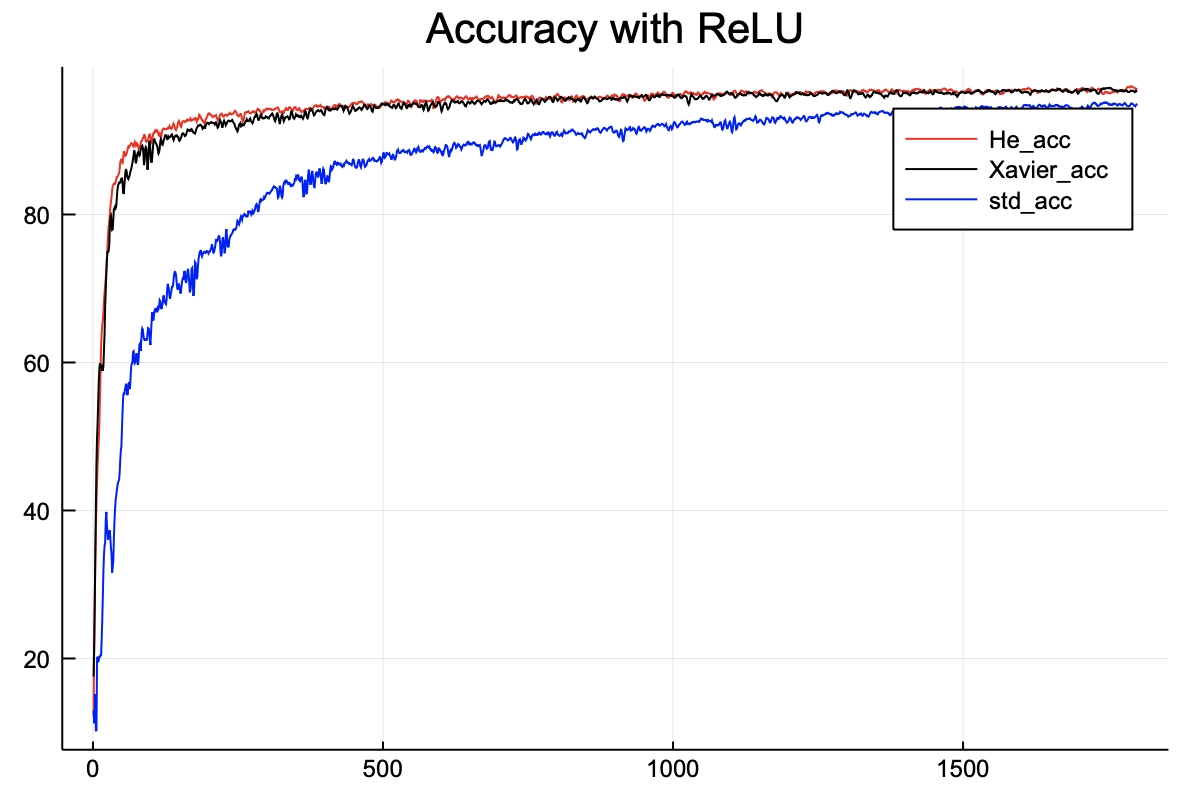
위 그래프는 ReLU 기반 4층 신경망의 정확도를 보여준다. 확실히 std초기값보다 다른 두 개의 초기값이 더 높은 정확도를 도출한다.

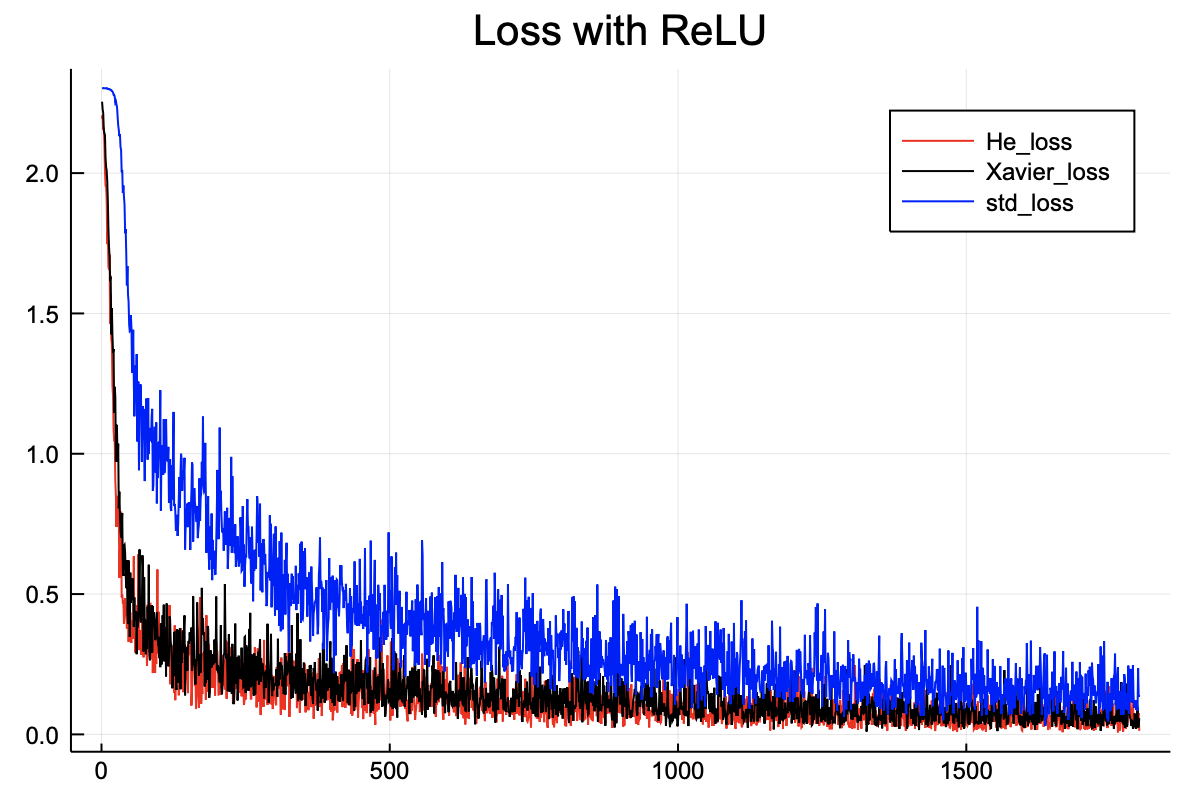
손실함수 또한 Xavier와 He 모두 훨씬 더 낮다.

위 그래프 결과로 유추해볼 수 있는 결론은 다음과 같다.

전체적으로 시그모이드 함수보다 ReLU 함수가 더 학습이 잘된다.
std초기값보다 Xavier나 He 초기값을 사용하는 것이 훨씬 효율적이다.
Xavier 초기값보다 He 초기값이 학습진도는 더 빠르다.

결론

이번 글에서는 다양한 가중치 초기값에 대해서 공부하였다. 그에 대한 결론은 다음과 같다.

얕은 신경망을 구현한다면 std를 써도 문제는 없다.
하지만 깊은 신경망을 구현한다면 Xavier와 He를 사용해야 한다.
해당 신경망의 활성화 함수가 시그모이드나 tanH과 같은 S자 함수일 때는 Xavier 초기값 사용하기
해당 신경망의 활성화 함수가 ReLU와 같은 비선형 함수일 때는 He 초기값 사용하기

다음 글에서는 오버피팅을 막아주는 드랍아웃(Dropout)에 대해서 살펴볼 것이다.