welcome :)

0%

14. CNN 시작하기

작성일 In ,

해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.

지금까지 우리는 다층퍼셉트론(MLP) 기반의 완전연결신경망(Fully Connected network)을 구현하면서 원리를 알아보았다. 하지만 이미지 데이터를 기반으로 신경망을 구현할 때, 완전연결신경망은 이미지 데이터를 일자로 펴서 학습하므로 데이터의 공간적 특성을 이해하기 어렵다. 이를 해결하기 위해 등장한 개념이 바로 합성곱(convolution)이다.

CNN (Convolutional Neural Network) 이란

‘합성곱 신경망(CNN, Convolutional Neural Network)’은 3차원의 이미지 데이터를 그대로 입력받아 학습하는 신경망이다. 완전연결신경망과 다른 점은 ‘합성곱(convolution)’과 ‘풀링(pooling)’이라는 레이어가 추가된다는 것이다. 따라서 CNN을 이해하기 위해서는 두 레이어의 원리를 알아야 한다.

합성곱 (Convolution)

합성곱은 하나의 이미지를 여러 조각으로 나누어 각 조각의 특성을 전달하는 방식이다. 아래의 그림은 합성곱의 원리를 보여준다. 참고로 깃허브에서 줄리아로 구현한 합성곱 코드를 볼 수 있다.

합성곱

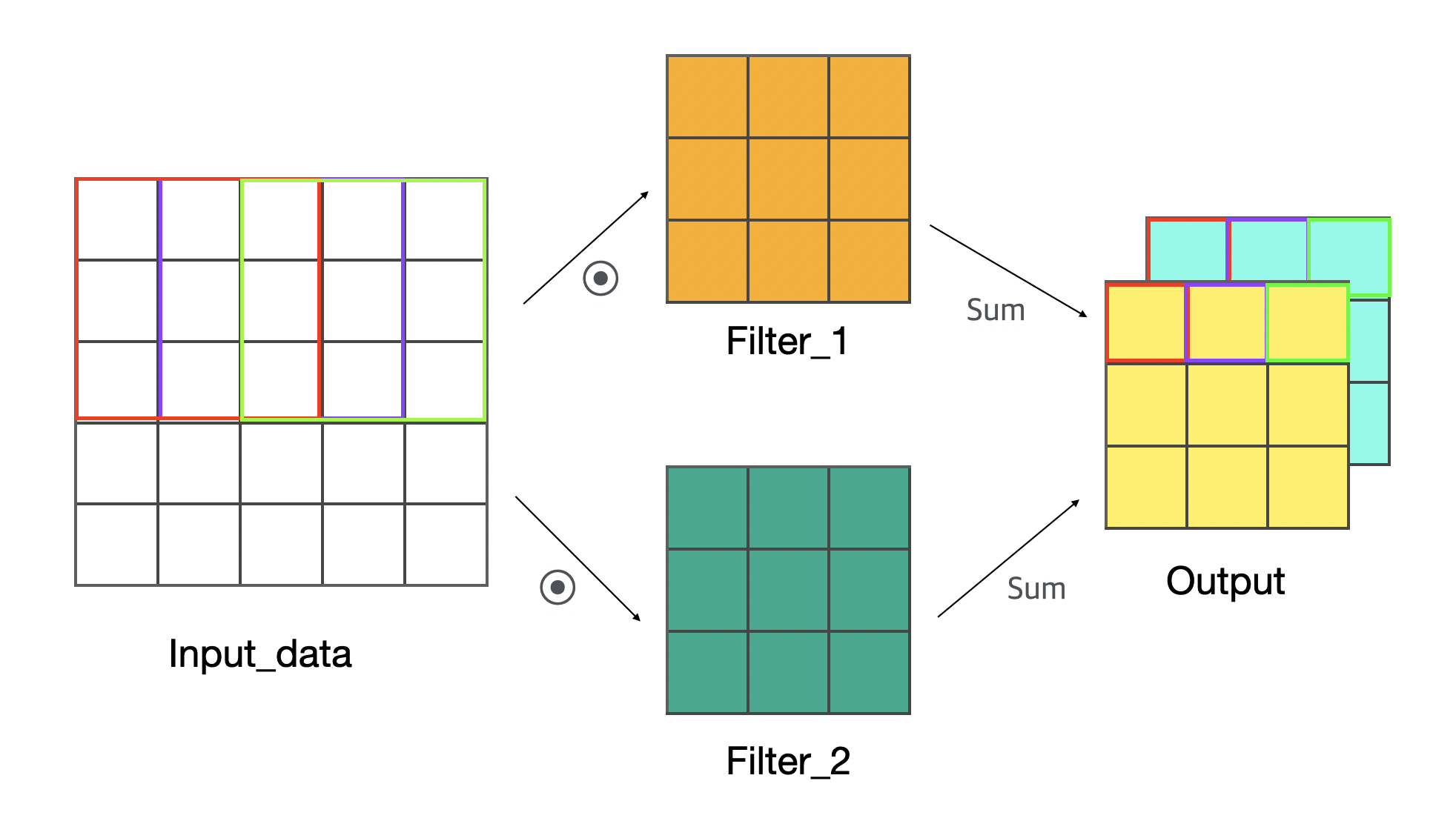
먼저 그림에서 Input_data는 입력된 이미지이고, Filter_1 와 Filter_2는 가중치이다. 합성곱층에서는 가중치 크기에 맞게 조각난 입력데이터들을 곱하여 합한 후 결과값 요소로 반환한다. 위의 예시는 다음과 같은 셋팅이다.

  • 입력데이터: $5 \times 5 \times 1 \times 1$ 배열인 4차원 데이터이다.
    기본적으로 이미지 데이터는 3차원으로 구성되어 있지만, 보통 배치데이터로 훈련하기 때문에 4차원이라고 보는 것이 더 좋다. 줄리아에서 배열의 순서는 행 $\times$ 열 $\times$ 색(차원) $\times$ 개수 이다. 여기서 색(차원)은 흑백인 경우 1, 컬러인 경우 RGB로 나뉘어 3이 된다.

  • 가중치(필터): $3 \times 3 \times 1 \times 2$ 배열인 4차원 데이터이다.
    가중치는 입력데이터와 곱해진다. 가중치의 배열 순서는 행 $\times$ 열 $\times$ 색(차원) $\times$ 개수으로 입력데이터와 동일하다. 참고로 가중치의 개수는 결과값의 차원이 된다.

입력데이터의 조각들과 가중치를 각각 곱한 후 그 곱들의 합이 결과값의 원소가 된다. 이미지를 조각내는 기준을 스트라이드(stride)라고 하며, 위의 예시는 스트라이드가 1인 경우이다.
또한 합성곱은 입력데이터보다 더 작은 크기의 결과를 반환한다. 결과값 행렬의 크기를 구하는 식은 다음과 같다.

위 식을 따라 위의 그림 예시의 값들을 넣어본다면 다음과 같다.

참고로 $padding$은 데이터 크기가 줄어드는 것을 막기 위해서 사용하는 방법이다.

Note
패딩 (padding) 이란?
패딩은 데이터에 표면에 0을 둘러서 데이터 크기를 키우는 기술을 의미한다. 예를 들어 $2 \times 2$ 행렬이 있고 패딩을 1 추가한다면, 모든 표면에 0이 둘러지면서 $4 \times 4$ 행렬을 반환한다.

결국 입력데이터 $5 \times 5 \times 1 \times 1$ 배열은 가중치 $3 \times 3 \times 1 \times 2$ 배열과 합성곱되어 결과값 $3 \times 3 \times 2 \times 1$ 배열을 도출한다. 이를 모두 정리하면 다음과 같다.

  • 입력데이터 형상: $5 \times 5 \times 1 \times 1$
  • 필터 형상: $3 \times 3 \times 1 \times 2$
  • 합성곱 결과 형상: $3 \times 3 \times 2 \times 1$

합성곱 결과의 배열 순서는 행 $\times$ 열 $\times$ 가중치 개수 $\times$ 입력값 개수이다. 즉, 가중치의 개수가 결과값의 차원이 되는 것이다.

풀링 (pooling)

풀링은 데이터의 크기를 줄여주는 방법이다. 데이터가 큰 경우 파라미터가 기하급수적으로 증가하여 연산 시간이 많이 소요된다. 이를 방지하고자 중간에 풀링 계층을 넣어 데이터의 크기를 줄여준다. 풀링은 크게 ‘최대값 풀링(Max pooling)’과 ‘평균 풀링(Average pooling)’이 있다. 보통 최대값 풀링이 많이 사용된다. 깃허브에서 줄리아로 구현한 풀링 코드를 볼 수 있다.

최대값 풀링 (Max pooling)

최대값 풀링의 원리를 그림으로 나타내면 다음과 같다.

최대 풀링

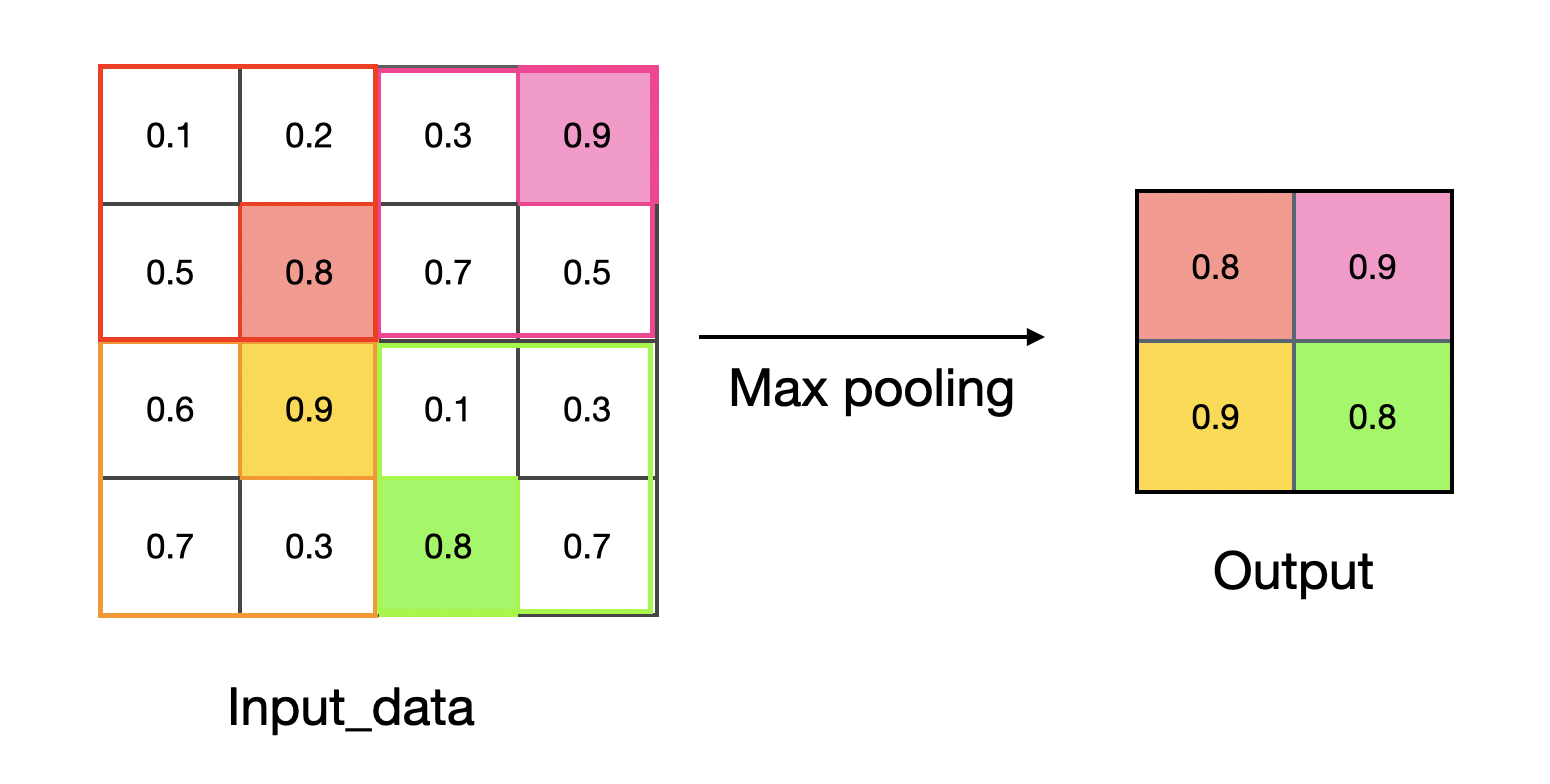
풀링에서는 합성곱과 달리 필터가 필요하지 않다. 다만, 풀링의 범위를 정해야 한다. 위의 그림에서는 $2 \times 2$ 크기로 풀링을 진행하며, 해당 범위에서 최대값을 반환하는 것이 최대값 풀링이다.

평균 풀링 (Average pooling)

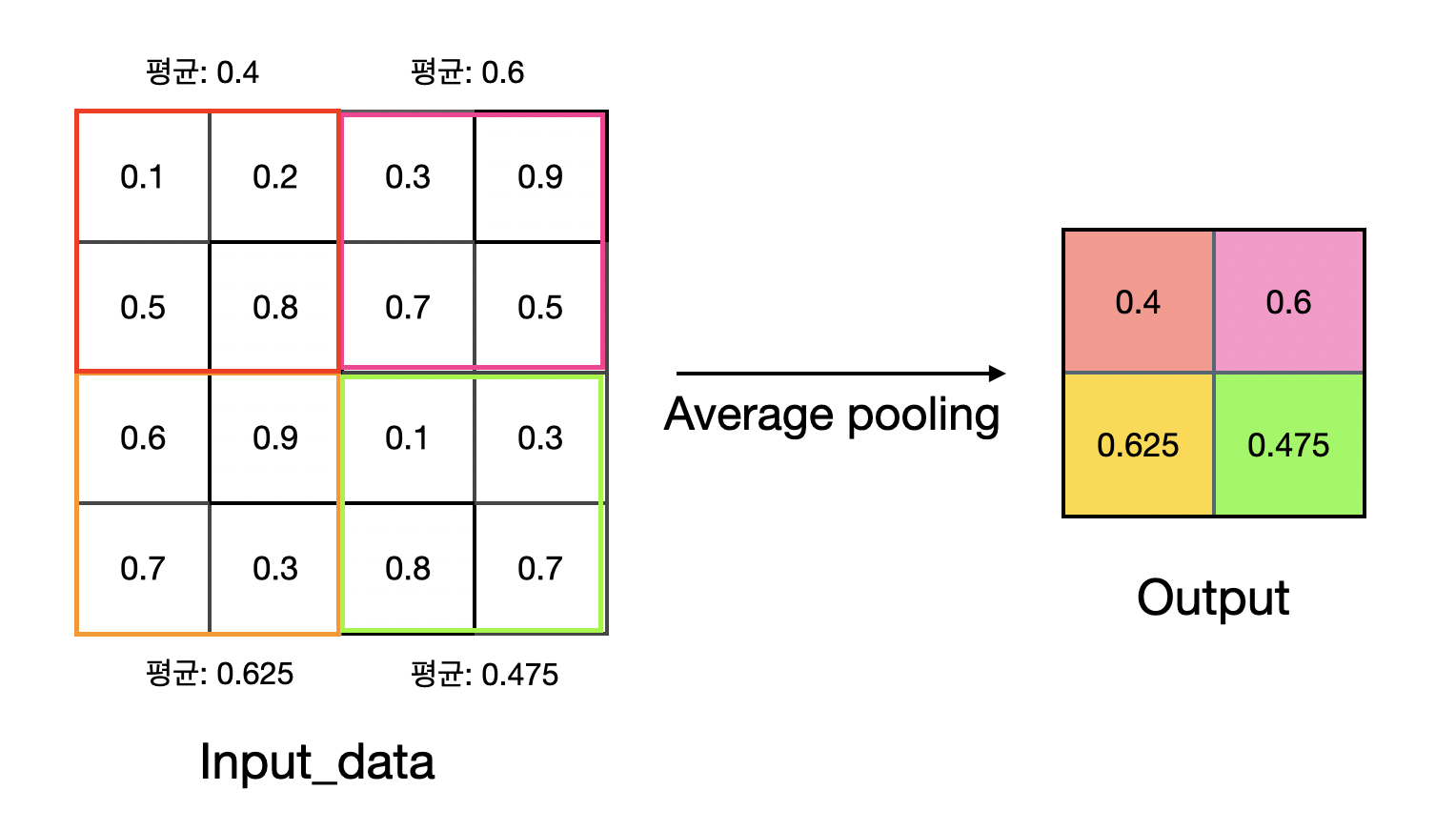
평균 풀링은 풀링 크기의 요소들의 평균을 결과값으로 반환한다. 그림으로는 다음과 같다.

평균 풀링

Simple CNN 구현

지금까지 합성곱층과 풀링층의 원리에 대해서 알아보았다. 이제 실제 코드로 구현하여 신경망을 학습해보자.

준비 단계

먼저 깃허브에 들어가서 해당 clone이나 Download zip을 하여 코드들을 저장해야 한다.
만약 이에 대해 잘 모르거나 어려운 사람들은 해당 페이지에서 코드를 직접 복사해서 입력할 수도 있다.

깃허브 데스크탑에 코드를 클론하거나 저장한 분들은 현재 사용하고 있는 커맨드의 경로를 CNN 파일로 변경해야 한다.

1
2
pwd # 현재 경로 확인
cd 코드가 있는 파일 경로 입력/Machine_Learning_in_Julia/CNN

다시 pwd를 입력했을 때 아래와 같이 변경되어 있으면 변경이 완료된 것이다.

1
/Users/코드가 있는 파일 경로/Machine_Learning_in_Julia/CNN

변경이 완료된 후 아래의 코드를 입력하자.

1
2
3
4
5
include("MNIST_data.jl")
include("functions.jl")
include("layers_without_im2col.jl")
include("making_network.jl")
include("optimizers.jl")

위 코드는 파일에 들어 있는 모든 코드들을 작동시킨다. 만약 코드를 복사하여 사용할 분들은 해당 페이지에서 위의 파일들의 코드를 복사하여 입력해주면 된다.

이제 간단한 CNN 모델을 만들 준비가 끝났다.

모델 설계

합성곱 신경망 1층과 완견연결 신경망 2층을 사용하여 모델을 구성하고자 한다. 모델의 순서는 다음과 같다.

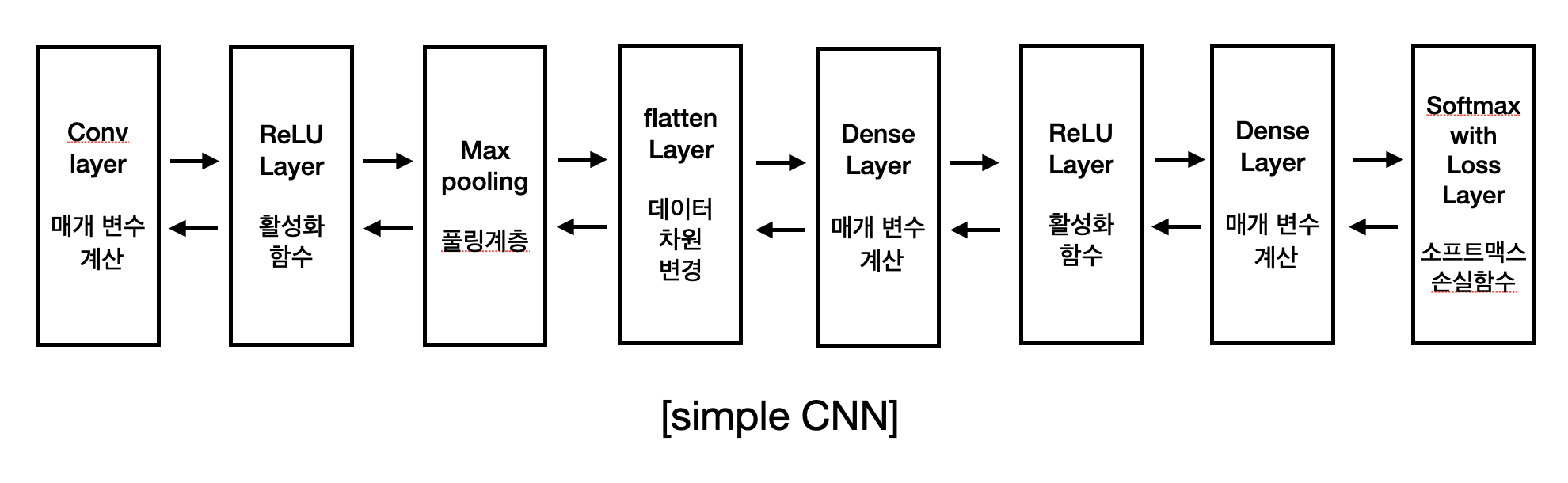
simple CNN

위 모델은 책 ‘밑바닥부터 시작하는 딥러닝’에서 예제로 사용한 것이다. 매우 간단하지만 MNIST 데이터를 학습하는 데 문제가 없다. 이제 모델 층에 알맞은 predict()를 정의해야 한다.

1
2
3
4
5
6
7
8
9
10
11
function  predict(input)

    pconv_1 = conv2D_forward_batch(pre_dense, input, params["W1"], params["b1"],1)
    pconv_Re = relu.(pconv_1)
    ppool_1 = maxpooling2D_forward_batch(pre_pool,pconv_Re, 2, 2)
    flatten_1 = flatten_forward_batch(pre_flatten,ppool_1)
    dense_1 = (flatten_1 * params["W2"]) .+ params["b2"]
    dense_relu = relu.(dense_1)
    dense_2 = (dense_relu * params["W3"]) .+ params["b3"]
    result = softmax(dense_2)
end

학습 구현

loss()에 사용되는 예측 함수를 설정한 후에 파라미터인 가중치와 편향 초기값도 설정한다.

1
2
3
4
5
6
W =["W1","W2","W3"]
b = ["b1","b2","b3"]
weight_size = [(5,5,1,30),(4320,100),(100,10)];
input_size = (28,28,1)

params = making_network(W, b, weight_size,input_size,"std");

초기값은 기본값으로 사용하는 std로 설정하였다. 초기값에 대해서는 인공신경망 최적화 - 가충치 초기값에서 더 자세히 알 수 있다.

파라미터를 만들었다면, 이제 모델에서 필요한 값들을 저장할 저장소를 생성한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# predict()용 저장소
pre_dense = dense_layer(0,0,0,0,0,0)
pre_pool= repository(0,0,0)
pre_flatten = repository(0,0,0)


# 실제 저장소
result = SoftmaxwithLoss(0,0)
dense1 = dense_layer(0,0,0,0,0,0)
dense2 = dense_layer(0,0,0,0,0,0)
dense3 = dense_layer(0,0,0,0,0,0)
Relu1 = repository(0,0,0)
Relu2 = repository(0,0,0)
optimizer = optimizers(0,0,0,0)
pool1= repository(0,0,0)
flatten1 = repository(0,0,0)

pre라고 붙은 저장소는 모델에 사용되는 함수의 파라미터 개수를 맞춰주기 위해 만든 것이다. 사실상 모델에 필요한 값을 저장하는 저장소는 아니다. 다음으로는 로스값과 미분값을 저장할 리스트와 딕셔너리를 정의한다.

1
2
grads = Dict()
train_loss_list= []

이제 모델을 작동시켜보자. 해당 모델의 구성은 다음과 같다.

  • Algorithm: backpropagation
  • Optimizer: Adam
  • batch_size: 100
  • one_epoch: 600
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
@time begin
    for i in 1:600

        batch_size = rand(1:size(train_x)[4],100)
        train_x_batch = train_x[:,:,:,batch_size]
        t_batch = reshape(t[batch_size,:],100,10)

        #신경망 계산
        conv_1 = conv2D_forward_batch(dense1,train_x_batch,params["W1"],params["b1"],1)
        conv_Re = relu_forward(Relu1, conv_1)
        pool_1 = maxpooling2D_forward_batch(pool1, conv_Re, 2, 2)
        flatten_1 = flatten_forward_batch(flatten1, pool_1)
        dense_1 = dense_layer_forward(dense2,flatten_1,params["W2"],params["b2"])
        dense_relu = relu_forward(Relu2, dense_1)
        dense_2 = dense_layer_forward(dense3,dense_relu,params["W3"],params["b3"])
        num = SoftmaxwithLoss_forward(dense_2,t_batch)

        #역전파 알고리즘
        last_layer = SoftmaxwithLoss_backward(result)
        dense_2_back = dense_layer_backward(dense3, last_layer)
        grads["W3"] = dense3.dw
        grads["b3"] = dense3.db
        dense_relu_back = relu_backward(Relu2, dense_2_back)
        dense_1_back = dense_layer_backward(dense2, dense_relu_back)
        grads["W2"] = dense2.dw
        grads["b2"] = dense2.db
        flatten_1_back = flatten_backward_batch(flatten1,dense_1_back)
        pool_1_back = maxpooling2D_backward_batch(pool1, flatten_1_back, 2, 2)
        conv_Re_back = relu_backward(Relu1, pool_1_back)
        conv_back = conv2D_backward_batch(dense1,conv_Re_back)
        grads["W1"] = dense1.dw
        grads["b1"] = dense1.db

        #가중치 갱신
        Adam(params,grads)

        temp_loss = loss_CNN_batch(train_x_batch,t_batch)
        print("NO.$i: ")
        println(temp_loss)
        append!(train_loss_list, temp_loss)
    end
end

위 모델의 정확도는 다음과 같다.

1
2
3
4
5
# 1에폭: 96.8
# 2에폭: 97.73
# 3에폭: 98.35
# 4에폭: 98.39
# 5에폭: 98.50999999999999

확실히 MLP보다 학습이 잘 된다는 것을 확인할 수 있다.

결론

위 코드는 1에폭(600)에 1시간 정도 소요된다. 이전까지 배웠던 MLP 모델을 작동시켜봤다면 ‘이 모델이 역전파를 사용한 것이 맞는가?’ 라는 의문이 들 수 있다.
사실 위 모델에 사용된 방식의 합성곱층과 풀링층은 이론적으로는 맞지만, 아무도 사용하지 않는다. 그 이유는 너무 느려서이다. 4차원 데이터를 가공하지 않고 인덱스를 잡아 함수를 실행하는 것은 컴퓨터의 입장에서 엄청난 노동이다. 그래서 우리는 기술적으로 4차원 데이터를 2차원으로 변환한 뒤, 계산을 하고 다시 4차원으로 조립하는 과정을 사용한다.
이 방법은 아~~주 느린 합성곱층과 풀링층을 훨씬 빠르게 작동하게 만들어준다.

만약 위 코드를 1에폭이라도 돌려봤다면 그 필요성을 실감할 것이기에, 한 번쯤 돌려보기를 권장한다. 앞서 설명했던 차원을 변경해주는 함수는 일반적으로 동일한 이름으로 쓰인다. 순방향에서는 im2col(), 역방향에서는 col2im()이다. 의미는 이미지에서 행렬로, 또 행렬에서 이미지로 변경해준다는 의미이다. 즉, 4차원 데이터를 2차원으로, 2차원 데이터를 4차원으로 변경해준다는 의미와 동일하다.

다음 글에서는 im2col()과 col2im()의 원리를 설명하고, 줄리아로 구현해볼 것이다. 또한 이를 바탕으로 합성곱층과 풀링층의 함수를 구현할 것이다.