[10/18] ReLU vs. Sigmoid 성능 비교

해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.

우리는 이전 장에서 활성화 함수로 시그모이드를 사용한 2층 신경망 학습을 구현하였다. 그렇다면 ReLU를 기반으로 한 신경망과 어떤 차이가 있을까? 이번 글에서는 두 활성화 함수의 성능을 비교할 것이다. 만약 활성화 함수에 대해서 더 공부하고 싶다면 이 글을 참고하면 된다.

먼저 간단하게 시그모이드와 ReLU 함수를 복습해보자.

시그모이드 함수

시그모이드 함수는 입력값들을 \(0\)과 \(1\)사이의 수로 변환해주는 함수이다. 수식은 아래와 같다.

\[h(x)=\frac{1}{1+e^{-x}}\]

위의 수식에서 볼 수 있듯이 시그모이드는 지수 함수로 이루어져 있다. 그래서 비교적 계산이 복잡하며, 계산량이 많을수록 느려질 수밖에 없다. 만약 지수함수가 왜 느린지 알고 싶다면 이 글에서 자세히 살펴볼 수 있다.

ReLU 함수

ReLU 함수는 음수를 모두 \(0\)으로 바꾸고 양수는 그대로 출력하는 함수이다. 수식은 다음과 같다.

\[ h(x) = \begin{cases} 0 & \text{(x≤0)\]}\ x & \ \end{cases} $$

ReLU 함수는 x값을 그대로 보내거나 0을 보낸다는 점에서 복잡한 계산은 없다. 그렇기에 같은 조건에서 계산을 진행한다면 시그모이드 함수보다는 빠르며, 최근 많이 사용하는 활성화 함수 중 하나이다.

성능 비교

활성화 함수에 대해 간단하게 복습을 했으니 이제 두 함수를 비교해보자. 우리는 이번 시간에 세 가지의 항목을 기준으로 비교할 것이다. 바로 정확도(accuracy), 손실함수 값(loss value) 그리고 시간이다. 정확도는 높을 수록, 손실 함수 값은 낮을 수록, 시간은 적게 소요될수록 좋은 것이라고 판단할 것이다.

WARNING 이 글에서 진행하는 성능 비교는 2층 신경망이며, MNIST데이터를 기반으로 한 분류 모델이다. 다른 모델에서 성능은 이 글의 결과와 차이가 있을 수 있다.

먼저 비교를 위해서 활성화 함수를 제외한 나머지 조건들은 모두 동일하게 셋팅한다. 우리가 비교에 사용할 신경망은 2층 구조이며, 데이터는 이전 글에서도 사용한 MNIST 데이터를 사용한다. 또한 입력층은 784, 은닉층은 50, 출력층은 10으로 설정한다. 마지막으로 배치 사이즈는 100으로, 학습률은 0.1로 설정하여 기본 셋팅을 완료한다. 해당 케이스에서 1에폭은 600번이다. 기본 셋팅에 대해서 자세히 알고 싶다면 이 글에서 살펴볼 수 있다.

성능을 비교하는 과정은 다음과 같다.

  1. 각각 활성화 함수로 이루어진 2층 인공신경망을 1에폭 학습한다.

  2. 한 번 학습할 때마다 해당 신경망이 test데이터 10000개 중 몇 개를 맞추는지 파악하여 정확도를 측정한다.

  3. 손실 함수와 정확도를 그래프로 나타낸다.

비교 in 순전파 알고리즘

첫 번째로는 순전파 알고리즘을 학습에 사용한 신경망이다. 순전파 알고리즘 구현 방법에 대해서 알고 싶다면 인공신경망 구현 - 순전파 알고리즘에서 살펴볼 수 있다.

두 활성화 함수를 비교하기 위해서는 신경망 모델 생성에 필요한 함수와 구조체들을 정의해야 한다. 깃허브 페이지에 들어가면 코드를 확인할 수 있다. 참고로 순전파 알고리즘을 작동시키기 위해서는 MNSIT_data.jl과 forward_propagation.jl에 있는 코드를 정의해야 한다.

순전파에서 활성화 함수를 바꿔주기 위해서는 predict()를 변경해주면 된다. 나머지는 모두 동일하게 사용된다.

1
2
3
4
5
6
function predict(x)
    a1 = (x * params["W1"]) .+ params["b1"]
    z1 = sigmoid.(a1)
    a2 = (z1 * params["W2"]) .+ params["b2"]
    return softmax(a2)
end

위 코드는 predict()이다. 함수 중간에 보면 z1 부분에 시그모이드가 있는 것을 확인할 수 있다. 위의 함수로 진행하면 시그모이드 기반의 신경망 모델이 작동된다. 따라서 ReLU()를 사용할 때는 아래의 함수 정의로 사용해야 한다.

1
2
3
4
5
6
function predict(x)
    a1 = (x * params["W1"]) .+ params["b1"]
    z1 = relu.(a1)
    a2 = (z1 * params["W2"]) .+ params["b2"]
    return softmax(a2)
end

이제 준비가 끝났다. 학습을 진행해보자. 참고로 아래의 학습 코드는 바꿀 것이 없다. 활성화 함수를 변경하려면 위의 predict()만 변경하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
@time begin
    for i in 1:600
        batch_mask = rand(1:train_size, 100)
        x_batch = train_x[batch_mask, :]
        t_batch = t[batch_mask, :]
        TwoLayerNet_numerical_gradient(loss, x_batch, t_batch)

        SGD(params, grads)

        temp_loss = loss(x_batch, t_batch)
        print("NO.$i: ")
        println(temp_loss)
        append!(train_loss_list, temp_loss)
        append!(accuracy, evaluate(test_x, test_y))
    end
end

우리는 @time을 사용했기에 학습이 끝나면 하단에 소요 시간이 나타난다. 두 함수에 따라 소요되는 시간은 다음과 같다.

1
2
sigmoid: 17632.126342 seconds
ReLU: 14847.352078 seconds

1에폭이었지만 시그모이드는 약 5시간, ReLU는 약 4시간 소요된 것을 확인할 수 있다. 시간 측면에서 성능은 ReLU의 승리이다.

또한 정확도인 accuracy와 손실함수값 리스트인 train_loss_list가 도출된다. 이를 사용한 활성화 함수에 따라 분리하여 저장하자.

1
2
3
4
5
6
7
# 시그모이드 기반 신경망 학습 후 저장
sig_forward_acc = vcat(accuracy)
sig_forward_loss = vcat(train_loss_list)

# ReLU 기반 신경망 학습 후 저장
relu_forward_acc = vcat(accuracy)
relu_forward_loss = vcat(train_loss_list)

이후 Plots를 사용하여 그래프를 그리면 아래와 같은 결과가 도출된다.

1
2
3
4
5
6
7
8
9
10
11
12
x = range(1,length(relu_forward_acc),step=1)
data = [relu_forward_acc sig_forward_acc]
labels = ["ReLU_acc" "sigmoid_acc"]
markercolors = [:red :blue]

for_acc=plot(
    x,
    data,
    label = labels,
    color = markercolors,
    markersize = 2,
    title = "Accuracy in Forward propagation")
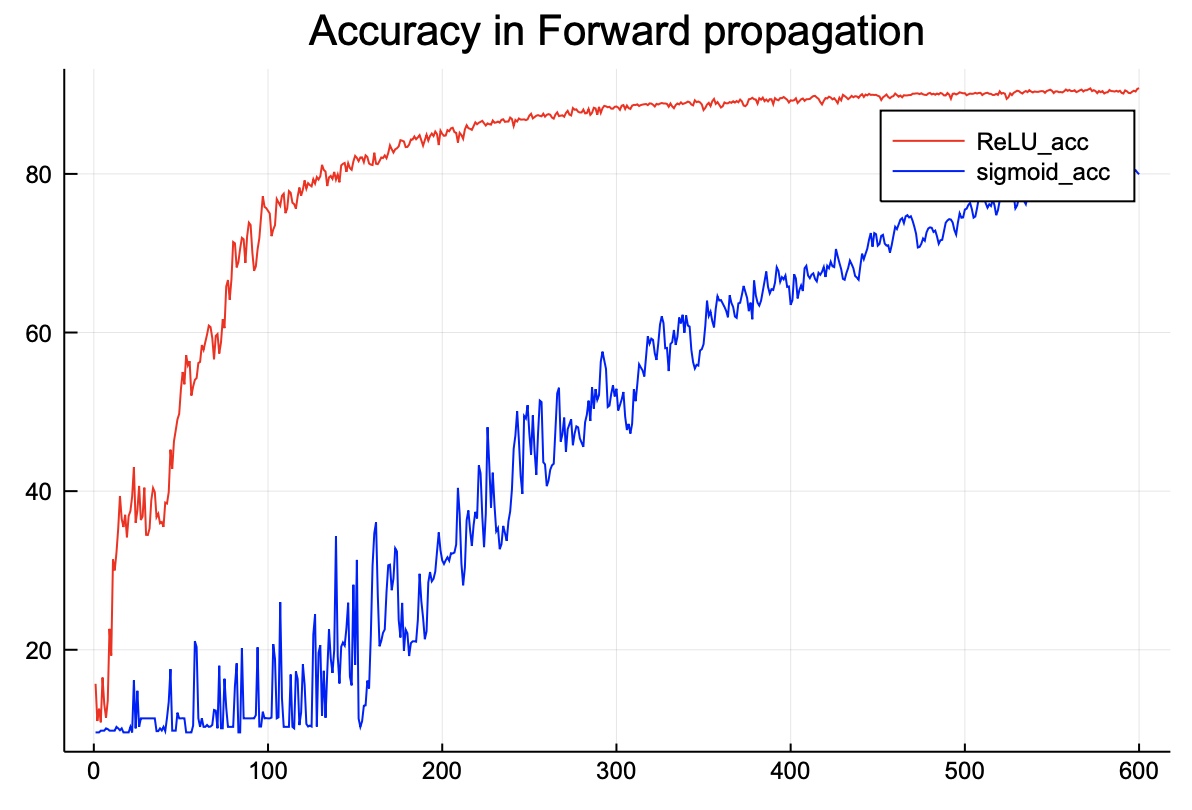
순전파 정확도

정확도를 비교해보면 ReLU 함수가 더 높은 것을 확인할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
x1 = range(1,length(relu_forward_loss),step=1)
data1 = [relu_forward_loss sig_forward_loss]
labels = ["ReLU_loss" "sigmoid_loss"]
markercolors = [:red :blue]

for_acc=plot(
    x3,
    data3,
    label = labels,
    color = markercolors,
    markersize = 2,
    title = "Loss in Forward propagation")
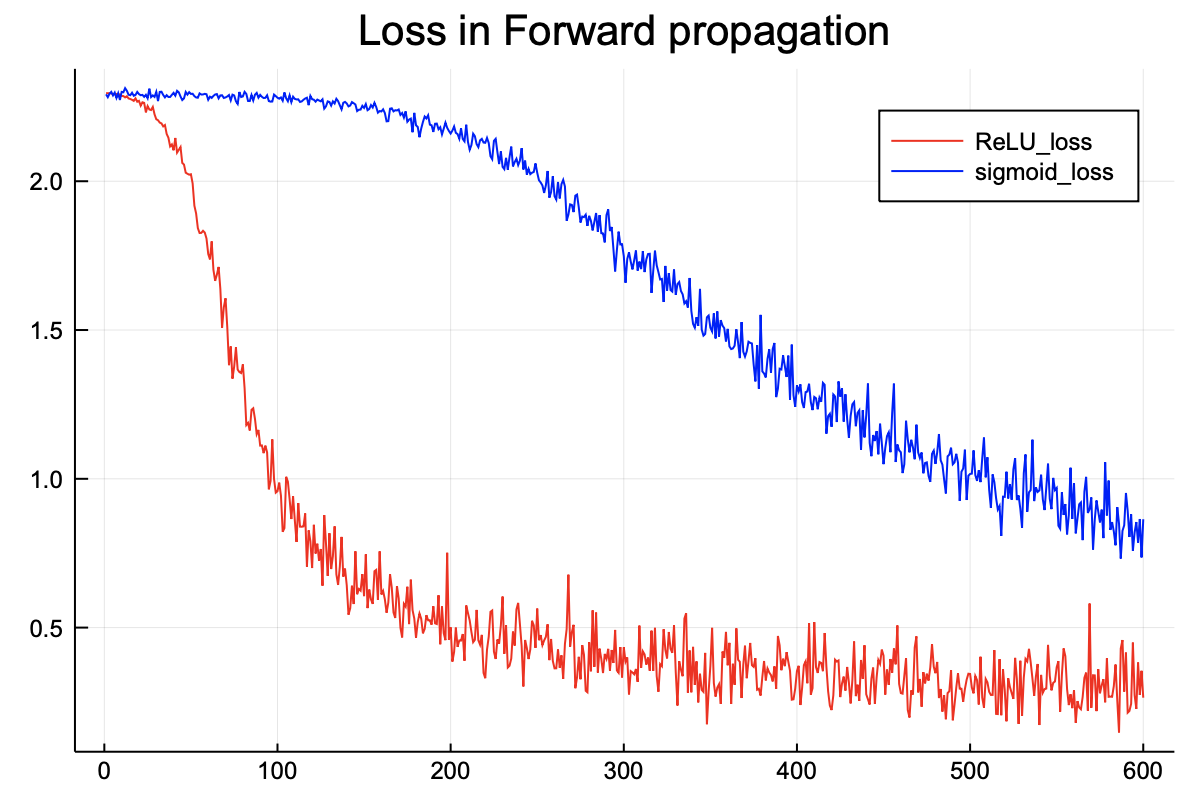
순전파 손실함수

손실함수 또한 ReLU가 더 낮다. 즉 순전파에서 ReLU의 완벽한 승리이다.

비교 in 역전파 알고리즘

지금부터는 이전 글에서 만들었던 역전파 알고리즘을 사용하여 신경망 모델을 학습시킬 것이다. 역전파 알고리즘 구현 방법에 대해서 알고 싶다면 인공신경망 구현 - 역전파 알고리즘에서 살펴볼 수 있다. 또한 역전파의 경우 개념이 추상적이라서 원리를 더 정확히 이해하고 싶다면 인공신경망 구현 - 역전파 설명을 읽어보기를 추천한다.

순전파와 마찬가지로 두 활성화 함수를 비교하기 위해서는 신경망 모델 생성에 필요한 함수와 구조체들을 정의해야 한다. 깃허브 페이지에 들어가면 코드를 확인할 수 있다. 역전파 알고리즘 또한 작동시키기 위해서는 MNSIT_data.jl과 backward_propagation.jl에 있는 코드를 정의해야 한다.

역전파 알고리즘에서 활성화 함수를 변경하기 위해서는 3가지를 체크해야 한다.

  • predict() 함수 내에 있는 활성화 함수
  • 신경망 계산에 속해 있는 활성화 함수 층(layer)
  • 역전파 알고리즘에 속해 있는 활성화 함수 층(layer)

predict()의 경우는 순전파와 똑같기 때문에 설명은 생략하고, 나머지를 변경해보자. 우선 역전파 알고리즘을 살펴보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
@time begin
    for i in 1:600
        batch_mask = rand(1:train_size, 100)
        x_batch = train_x[batch_mask, :]
        t_batch = t[batch_mask, :]

        # 신겸망 계산
        z1 = dense_layer_forward(dense1,x_batch,params["W1"],params["b1"])
        a1 = sigmoid_forward(Sigmoid1,z1) # 활성화 함수 층
        z2 = dense_layer_forward(dense2,a1,params["W2"],params["b2"])
        num = SoftmaxwithLoss_forward(z2,t_batch)

        # 역전파
        last_layer = SoftmaxwithLoss_backward(result)
        z2_back = dense_layer_backward(dense2, last_layer)
        grads["W2"] = dense2.dw
        grads["b2"] = dense2.db
        a1_back = sigmoid_backward(Sigmoid1, z2_back) # 활성화 함수 층
        z1_back = dense_layer_backward(dense1, a1_back)
        grads["W1"] = dense1.dw
        grads["b1"] = dense1.db

        #가중치 갱신
        SGD(params, grads)

        temp_loss = loss(x_batch, t_batch)
        print("NO.$i: ")
        println(temp_loss)
        append!(train_loss_list, temp_loss)
        append!(accuracy, evaluate(test_x, test_y))
    end
end

위 코드에 두 개의 활성화 함수 층이 있다. 이 함수를 시그모이드나 ReLU로 변경하면 된다. 위 코드는 시그모이드가 현재 활성화 함수로 사용되고 있다.

해당 학습을 진행하면 결과로 시간이 나온다. 역전파 알고리즘에서 1에폭 당 소요되는 시간은 다음과 같다.

1
2
relu_back : 16.509151 seconds
sigmoid_back : 19.750770 seconds

역전파 또한 시그모이드 함수보다 ReLU 함수가 더 빠른 것을 확인할 수 있다. 역전파에서도 시간 측면에서의 성능은 ReLU의 승리이다.

또한 정확도인 accuracy와 손실함수값 리스트인 train_loss_list가 도출된다. 이를 사용한 활성화 함수에 따라 분리하여 저장하자.

1
2
3
4
5
6
7
# 시그모이드
sig_backward_acc = vcat(accuracy)
sig_backward_loss = vcat(train_loss_list)

# ReLU
relu_backward_acc = vcat(accuracy)
relu_backward_loss = vcat(train_loss_list)

이후 Plots를 사용하여 그래프를 그리면 아래와 같은 결과가 도출된다.

1
2
3
4
5
6
7
8
9
10
11
12
x2 = range(1,length(relu_backward_acc),step=1)
data2 = [relu_backward_acc sig_backward_acc ]
labels = ["ReLU_acc" "sigmoid_acc"]
markercolors = [:red :blue]

for_acc=plot(
    x2,
    data2,
    label = labels,
    color = markercolors,
    markersize = 2,
    title = "Accuracy in Backward propagation")
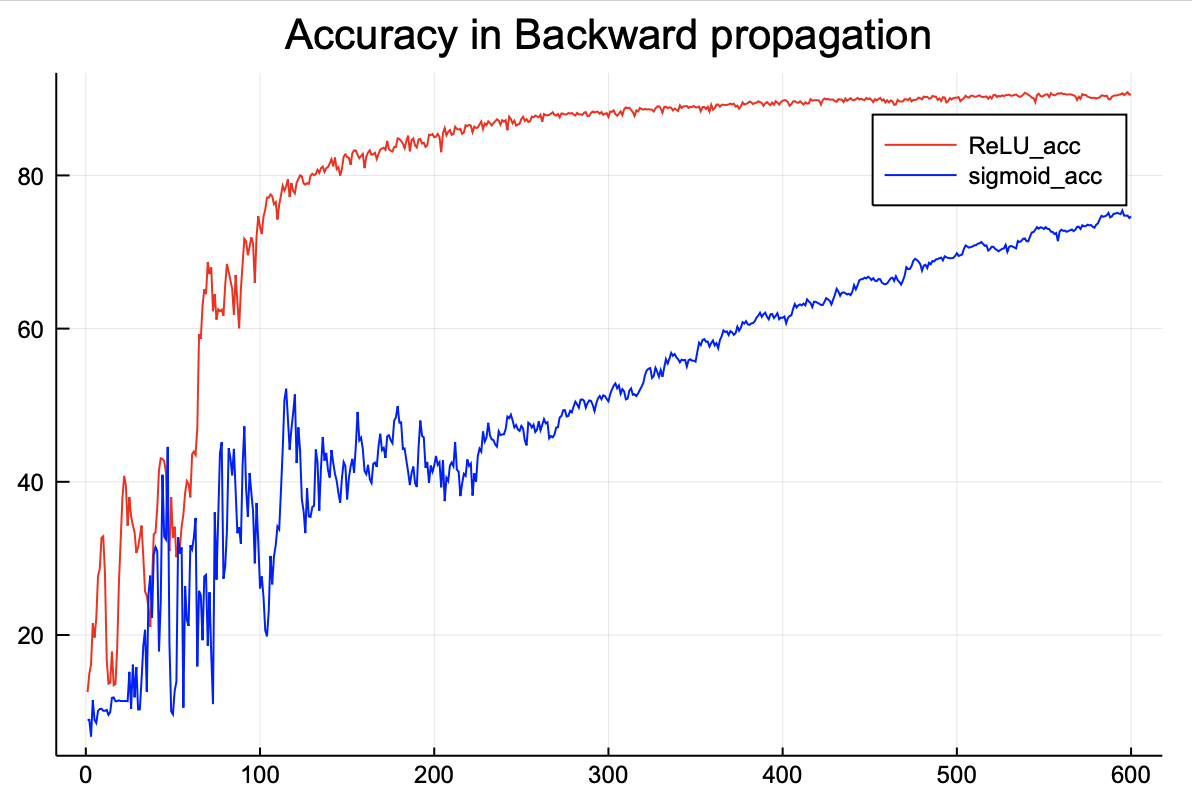
순전파 정확도

정확도를 비교해보면 ReLU 함수가 더 높은 것을 확인할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
x3 = range(1,length(relu_backward_loss),step=1)
data3 = [relu_backward_loss  sig_backward_loss]
labels = ["ReLU_loss" "sigmoid_loss"]
markercolors = [:red :blue]

for_acc=plot(
    x3,
    data3,
    label = labels,
    color = markercolors,
    markersize = 2,
    title = "Loss in Backward propagation")
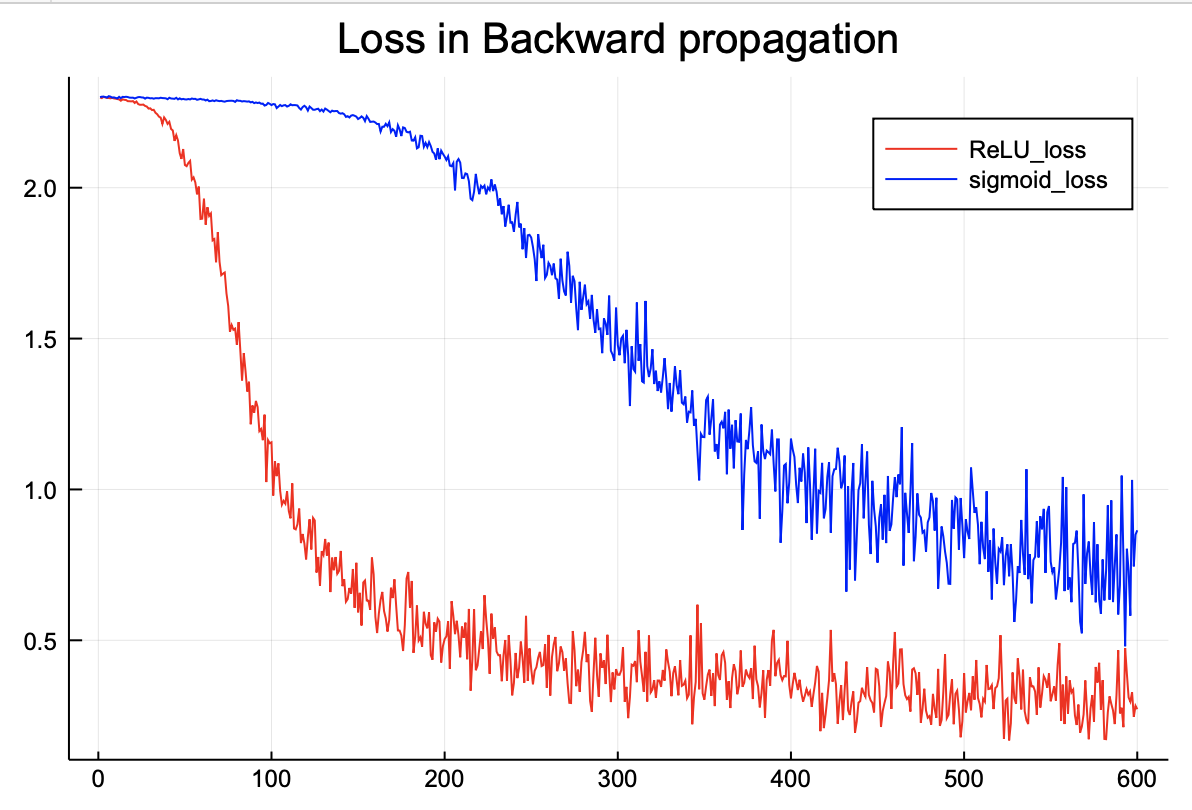
순전파 손실함수

손실함수 또한 ReLU가 더 낮다. 역전파에서도 ReLU의 완벽한 승리이다.

결론

지금까지 순전파와 역전파 알고리즘에서 어떤 활성화 함수가 학습을 잘 진행하는지, 또 실제 모델로서 잘 예측하는지를 비교해보았다. 결론은 간단한다.

ReLU가 짱이다!

SeriesHub > deep learning in julia
#딥러닝 #Deeplearning #머신러닝 #줄리아 #신경망 #ReLU #렐루 #시그모이드 #Sigmoid #활성화 함수
[10/18] ReLU vs. Sigmoid 성능 비교
https://dev-bearabbit.github.io/ko/DeeplearningJulia/Deeplearning-10/
Author
Jess
Posted on
2020년 5월 2일
Licensed under