[5/18] 인공신경망 구현: 수학식 풀이
해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.
인공신경망이란
\[Layer=(X*W)+B\]
위 수식은 각 층을 계산하는 식이며, 입력 데이터의 값들인 배열 \(X\)에 가중치 \(W\)를 곱한 후 편향 \(B\)를 더한다. 이 식은 신경망이 작동하는 방식에서 가져온 알고리즘이다. 생물학에서의 신경망은 수많은 뉴런(신경 세포)이 연결되어 있으며, 이들은 전기 신호를 전달한다. 각각의 뉴런들은 수상돌기를 통해 들어오는 전기 신호를 받고 세포체에서 종합한 후 축삭돌기를 통해 전기 신호를 다른 뉴런으로 내보낸다. 이때 축삭돌기 끝 부분인 시냅스에서 전기 신호에 따라 신경전달물질을 분비하여 다른 뉴런의 시냅스로 전달하는데 이런 과정을 신경이라고 부르는 것이다.
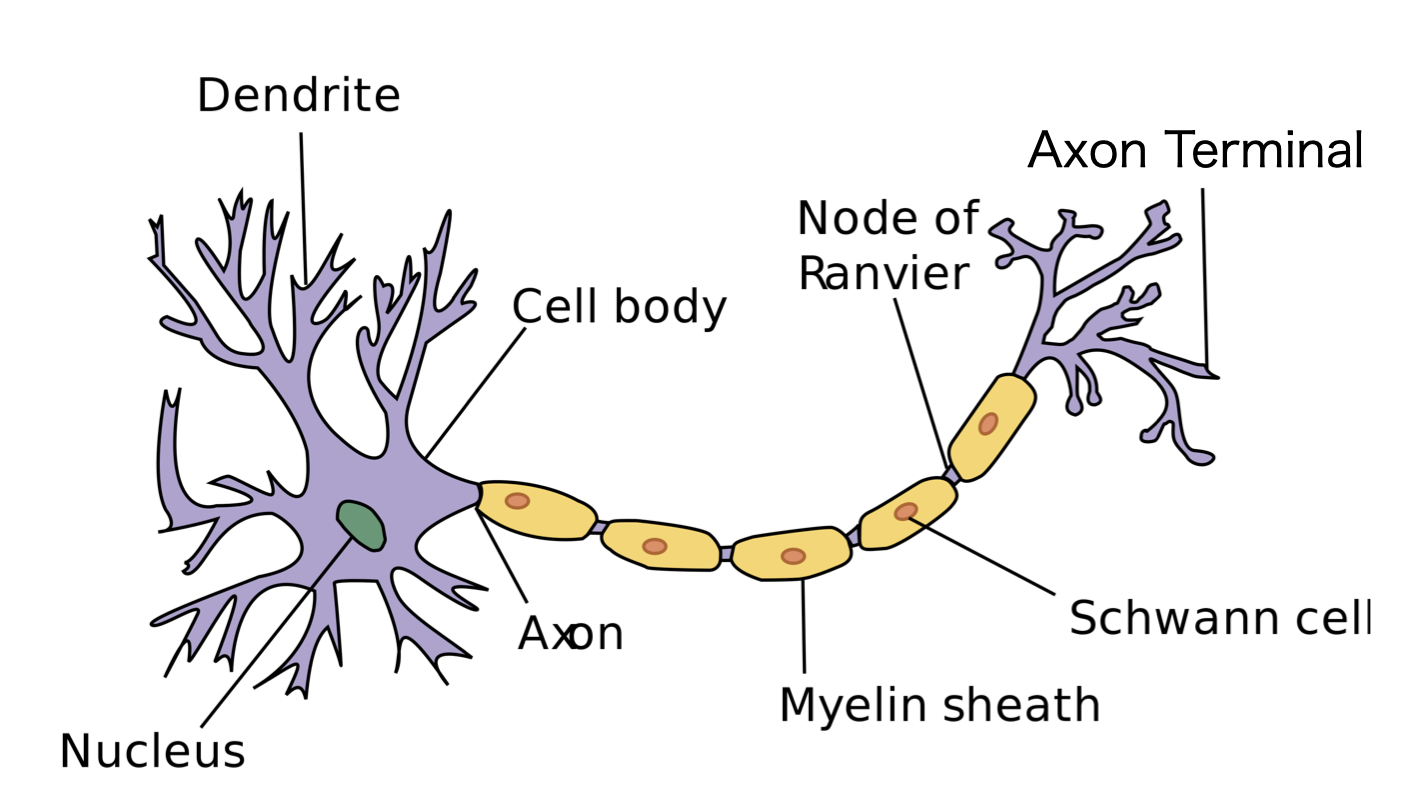
그렇다면 뉴런들은 왜 전기 신호들을 전달하는 것일까? 이유는 간단하다. 우리 몸에서 필요한 생활 기능들을 '적절'하게 조절하기 위해서이다. 뉴런은 수상돌기에서 전기 신호를 생산하라는 흥분성 신호와 전기 신호를 생산하지 말라는 억제성 신호를 받아들인다. 그후 세포체에서 이를 종합하여 다른 뉴런으로 해당 전기 신호를 보낼지 말지 결정한다. 이런 뉴런의 원리를 바탕으로 살펴봤을 때 가중치를 곱하는 것은 뉴런에서 각각의 고유한 흥분성과 억제성 신호를 받아들이는 과정을 표현했다고 볼 수 있다. 물론 실제 생물학에서의 뉴런은 세포체에서 전기 신호를 보내거나(1), 보내지 않거나(0)라는 계단 함수의 개념으로 작동한다는 차이점이 있지만, 가중치의 원리는 동일하다. 또한 편향은 뉴런이 가지고 있는 '임계값'을 표현한 것이다. 세포체는 받은 전기 신호가 어느 임계값 이상이 되어야 전기 신호를 내보내는 데, 이를 나타낸 것이다.
따라서 인공신경망의 원리를 한번에 설명한다면, 입력 신호에 가중치를 곱하면서 적절한 전기 신호로 변환하여 받은 후, 편향(임계값)이 넘으면 전기 신호를 출력한다고 정리된다. 2층으로 구성된 인공신경망 계산 과정을 도식화하면 다음과 같다.
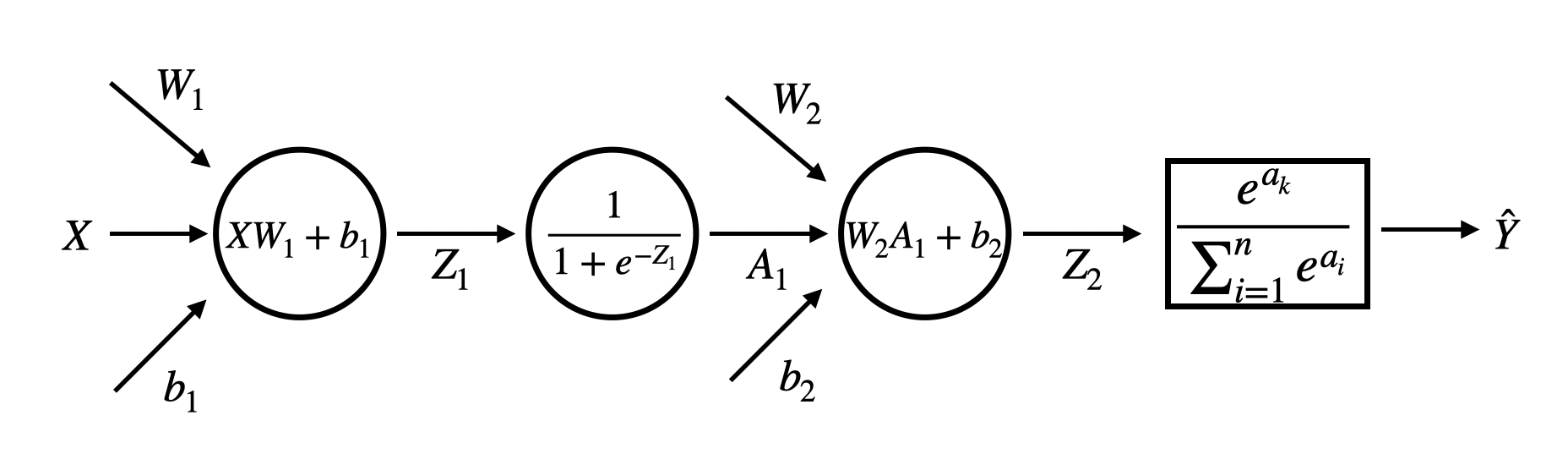
인공신경망 수학식 풀이
인공신경망을 코드로 구현하기에 앞서 수학식으로 풀이해보려고 한다. 이 과정이 필요한 이유는 컴퓨터가 신경망 모델을 어떻게 진행하는지 명확히 파악하고, 이해해야 하기 때문이다. 따라서 위의 인공신경망 도식을 수식으로 풀이해보자. (참고로 위의 인공신경망 도식은 2층 신경망이다.)
\[X: \begin{bmatrix} x_1 & x_2 \\ \end{bmatrix}\quad W_1: \begin{bmatrix} w1_{11} & w1_{12} \\ w1_{21} & w1_{22} \\ \end{bmatrix}\quad W_2: \begin{bmatrix} w2_{11} & w2_{12} & w2_{13}\\ w2_{21} & w2_{22} & w2_{23}\\ \end{bmatrix}\] \[B_1: \begin{bmatrix} b1_1 & b1_2 \end{bmatrix}\quad B_2: \begin{bmatrix} b2_1 & b2_2 & b2_3 \end{bmatrix}\]
먼저 입력값인 \(X\)와 가중치 \(W_1, W_2\), 편향 \(b_1, b_2\)를 설정한다. 예시이기 때문에 입력층, 은닉층, 출력층의 노드 개수를 임의로 설정하였다. (실제로는 훨씬 많은 노드들이 사용된다.)
\[Z1 = XW_1+B_1\] \[Z1= \begin{bmatrix} x_1 & x_2 \\ \end{bmatrix} \times \begin{bmatrix} w1_{11} & w1_{12} \\ w1_{21} & w1_{22} \\ \end{bmatrix} + \begin{bmatrix} b1_1 & b1_2 \end{bmatrix}\\\]
\[= \begin{bmatrix} x_1w1_{11}+x_2w1_{21}+b1_1 & x_1w1_{12}+x_2w1_{22}+b1_2 \end{bmatrix} \]
먼저 입력값에 첫 번째 가중치인 \(W_1\)을 곱하고 첫 번째 편향인 \(B_1\) 더한다. 입력값과 가중치, 편향 모두 배열이기에 이 계산은 배열 단위로 이루어진다. 즉, 행렬곱과 행렬덧셈이 사용되는 것이다. 이 과정은 입력값이 첫 번째 활성화 함수 \(h(x)\)로 넘어가기 전에 이루어진다.
\[A1 = \cfrac{1}{1+e^{-Z1}}\] \[A1 = \begin{bmatrix} \cfrac{1}{1+e^{-Z1_1}} & \cfrac{1}{1+e^{-Z1_2}} \end{bmatrix} \]
그 다음, 위의 \(Z_1\)을 활성화 함수에 대입하면 된다. 여기서 \(Z_1\)은 행렬인데 위의 수식을 \(Z_1\)의 요소에 각각 적용한다. 참고로 위 식에서 사용된 활성화 함수는 시그모이드 함수이다. 이 과정은 입력값이 첫 번째 은닉층에 도착한 것이다.
\[Z2 = A1 \times W_2+b_2\] \[ = \begin{bmatrix} \frac{w2_{11}}{1+e^{-Z1_1}}+\frac{w2_{21}}{1+e^{-Z1_2}}+b2_1 & \frac{w2_{12}}{1+e^{-Z1_1}}+\frac{w2_{22}}{1+e^{-Z1_2}}+b2_2 & \frac{w2_{13}}{1+e^{-Z1_1}}+\frac{w2_{23}}{1+e^{-Z1_2}}+b2_3 \end{bmatrix} \]
\(A1\)의 값은 행렬로 반환된다. \(A1\)을 다시 두 번째 은닉층으로 보내기 위해 두 번째 가중치인 \(W_2\)를 곱하고 두 번째 편향인 \(b_2\)를 더한다. 여기서도 행렬곱과 행렬덧셈이 사용된다. 행렬 단위로 계산되는 수식은 \(Z1\)과 동일하다.
\[\hat{y_k}=\cfrac{e^{Z2_k}}{\sum_{i=1}^n e^{Z2_i}}\] \[\hat{y}= \begin{bmatrix} \cfrac{e^{Z2_1}}{\sum_{i=1}^3 e^{Z2_i}} & \cfrac{e^{Z2_2}}{\sum_{i=1}^3 e^{Z2_i}} & \cfrac{e^{Z2_3}}{\sum_{i=1}^3 e^{Z2_i}} \end{bmatrix} \]
은닉층 계산 이후 마지막으로 출력층 활성화 함수인 소프트맥스 함수를 적용하여 예측값 \(\hat{y}\)을 얻는다.
위의 식을 토대로 우리는 예측값을 아래와 같은 식로 정의할 수 있다.
\[\hat{y}=\sigma(h(XW1+B1)\times W2+B2)\]
위의 식을 살펴보면 \(Z1\)인 \(XW_1+B_1\)을 활성화 함수 \(h(x)\)에 대입하고, 활성화 함수의 결과 값을 다시 \(Z2\)의 입력값으로 받는다. 그렇게 \(Z2\)를 계산한 후 출력층의 활성화 함수인 \(\sigma(x)\)에 대입하여 나온 값이 예측값 \(\hat{y}\)이다.
결론
아번 글에서는 신경망을 구현하기에 앞서 신경망의 원리를 수학식으로 풀이하였다. 이 과정은 이해를 위함이며, 다음 글에서는 손글씨 인식하는 신경망을 구현하면서 코드로 작동하는 과정을 살펴볼 것이다.