[8/18] 인공신경망 구현: 역전파 설명

해당 시리즈는 프로그래밍 언어 중 하나인 줄리아(Julia)로 딥러닝(Deep learning)을 구현하면서 원리를 설명합니다.

---

이전 글에서는 왼쪽 방향에서 오른쪽 방향으로 이동하는 미분법인 순전파 알고리즘을 살펴보았다. 순전파 알고리즘은 학습을 진행할 때마다 각각 매개변수의 미분값을 구해야 하기 때문에 신경망 계산이 매개변수 개수의 두 배가 진행된다. 이전 글에서의 신경망 모델을 예시로 보면 가중치와 편향이 총 4개이기 때문에 순전파 기반으로 학습을 한 번 할 때마다 신경망 계산은 총 8번 이루어진다. 이 방식은 매우 비효율적이고 시간이 오래걸린다. 순전파보다 더 효율적으로 미분하는 방법이 바로 역전파 알고리즘이다. 이번 장에서는 역전파 알고리즘에 대해서 살펴볼 것이다.

역전파란

역전파(backward propagation)는 순전파와 다르게 미분을 반대로 하는 것을 의미한다. 즉, 순전파는 왼쪽에서 오른쪽 방향으로 미분이 이루어진다면, 역전파는 오른쪽에서 왼쪽 방향으로 미분이 이루어진다. 도식에서 확인하자면 아래와 같다.

신경망 계산 방향

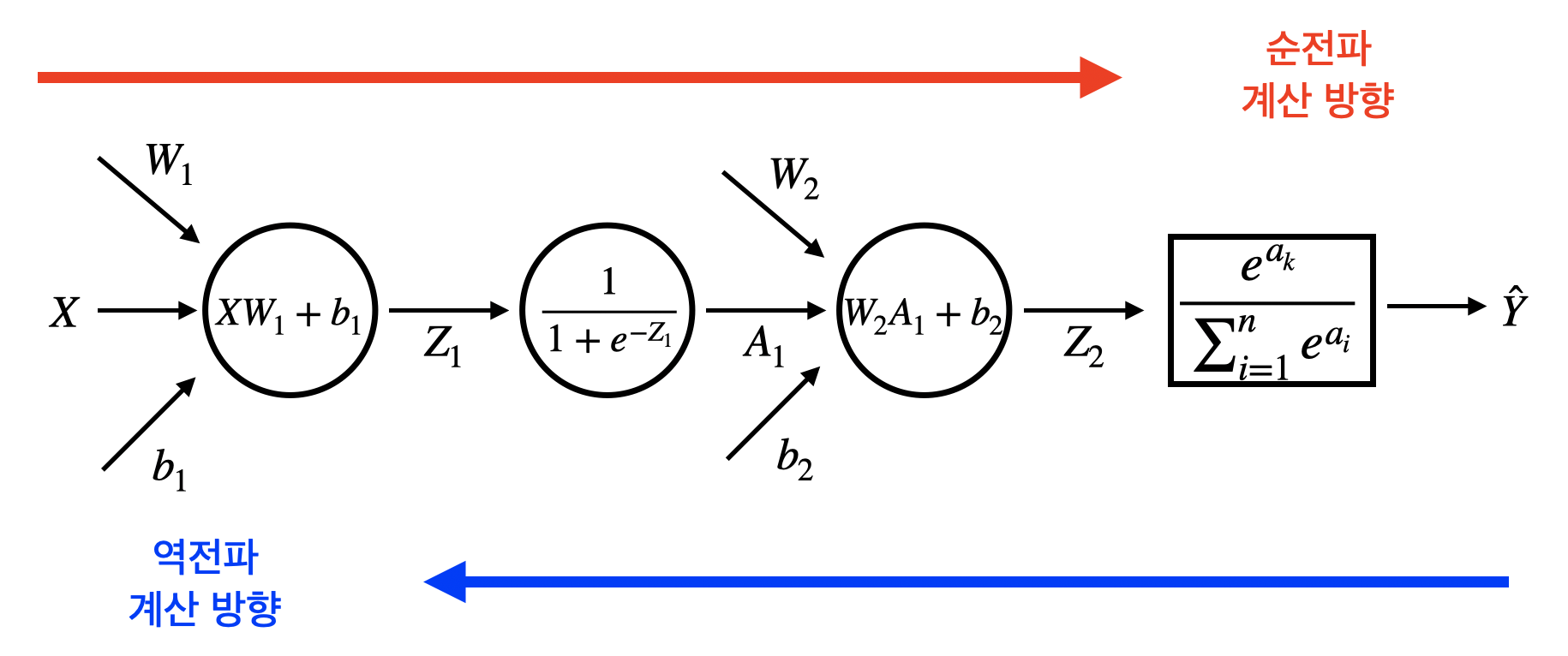
또한 순전파와 역전파는 신경망 계산이 이루어지는 과정도 약간 다르다. 우리가 만든 2층 신경망 모델의 순전파 알고리즘은 각각 가중치와 편향의 편미분 값을 구하기 위해서 신경망 계산이 8번 이루어지지만, 역전파 알고리즘은 한번 진행될 때 가중치와 편향의 편미분 값을 바로 구할 수 있다. 이것이 역전파가 순전파보다 훨씬 빠르게 진행되는 이유이다. 신경망 계산은 행렬 계산으로 이루어지기 때문에 매우 복잡하고 계산량이 많다. 따라서 계산을 여러 번 할수록 훨씬 많은 시간이 소요된다. 따라서 시간의 관점에서 역전파는 순전파보다 훨씬 더 효율적인 알고리즘이라고 볼 수 있다. 순전파와 역전파의 차이를 정리하면 다음과 같다.

미분 알고리즘 비교

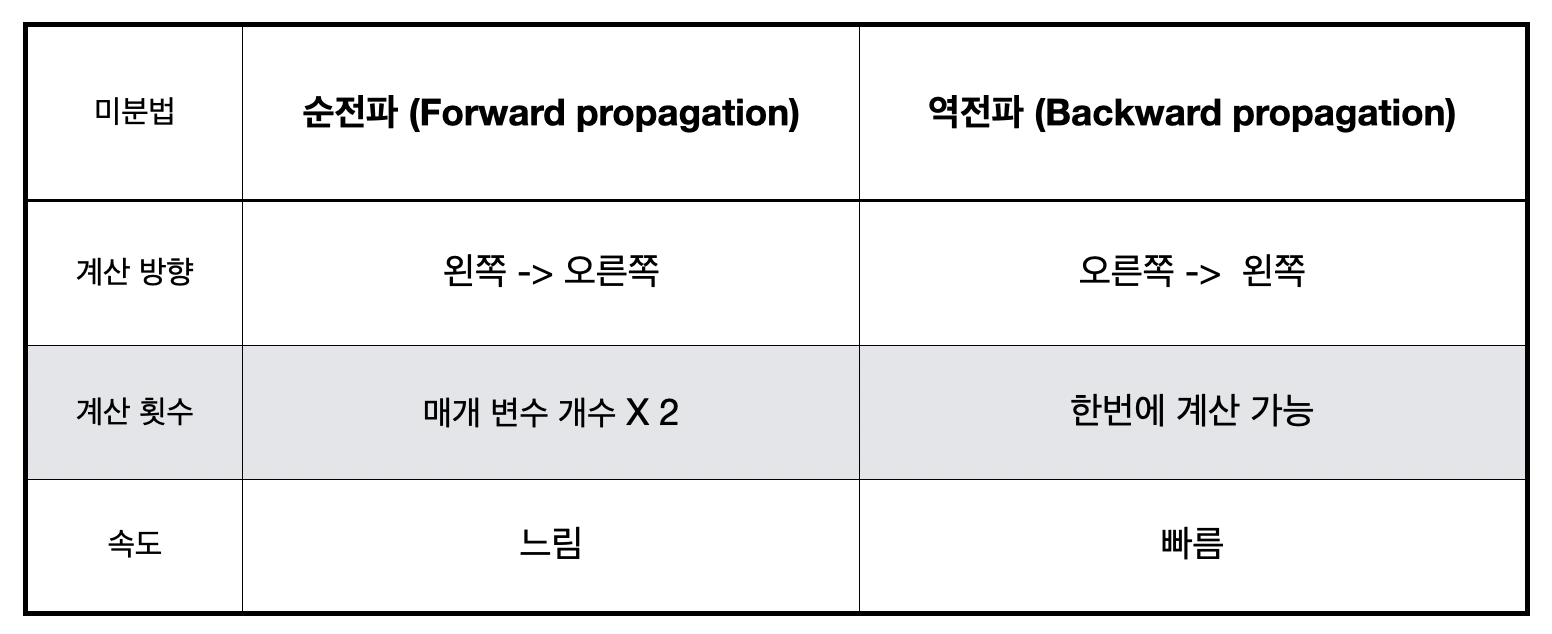
역전파의 원리: 합성함수의 미분

역전파가 한번에 편미분을 구할 수 있는 원리는 합성함수의 미분을 이용한 것이다. 먼저 우리가 만들었던 2층 신경망 모델의 수식을 확인해보자.

\[\hat{y}=\sigma(h(XW1+B1)\times W2+B2)\]

위의 수식을 다음과 같이 정리할 수 있다.

\[Z1=XW1+B1\\ A1 = h(Z1)\\ Z2=A1W2+B2\\ \sigma(Z2) = \hat{y}\]

위 수식은 신경망 계산 순서를 그대로 나열한 것이다. 순전파 알고리즘에서는 각각 매개변수를 편미분하여 예측값을 비교한다. 하지만 역전파 알고리즘은 위의 수식들을 미분한 식을 바탕으로 기존 매개변수들을 받아 각 매개변수들의 미분값을 한번에 계산한다.

즉, 역전파 알고리즘은 다음과 같다.

\[\partial\hat{y} = \partial\sigma(Z2)\\ \partial Z2= \partial(A1W2 + B2)\\ \partial A1 = \partial h(Z1)\\ \partial Z1 = \partial(XW1+B1)\]

위 순서는 합성함수의 미분이다. 합성함수는 변수가 두개 이상의 함수에 둘러싸인 경우를 의미한다. 예시로 아래의 사례를 보자.

\[ y = t^2 , t = x+2\]

위의 식 \(y\)에서 \(x\)를 미분하기 위해서는 중간의 \(t\)를 미분해야 한다. 따라서 다음과 같은 방법으로 미분된다.

\[\frac{dy}{dx}= \frac{dy}{dt} \cdot \frac{dt}{dx}\]

위의 미분식에서 \(dt\)는 약분되기 때문에 결국 \(\frac{dy}{dx}\)가 남는 것이다. 이를 정리하면 다음과 같다.

\[\begin{matrix} \frac{\partial y}{\partial x}& = & \partial (t^2) \times \partial t\\ &=& 2t \times \partial (x+2) \\ &=& 2(x+2) \times 1 \\ &=& 2x+4\\ \end{matrix}\]

이 방식을 2층 신경망 역전파 알고리즘에 대입하여 미분식을 구할 수 있다. 미분식은 아래와 같다.

\[\begin{matrix} \frac{\partial \hat{y}}{\partial W1}& = & \frac{\partial \hat{y}}{\partial Z2} &\times& \frac{\partial Z2}{\partial A1} &\times& \frac{\partial A1}{\partial Z1} &\times& \frac{\partial Z1}{\partial W1}\\ &&\\ \frac{\partial \hat{y}}{\partial W2}& = & \frac{\partial \hat{y}}{\partial Z2} &\times& \frac{\partial Z2}{\partial W2}\\ &&\\ \frac{\partial \hat{y}}{\partial b1}& = & \frac{\partial \hat{y}}{\partial Z2} &\times& \frac{\partial Z2}{\partial A1} &\times& \frac{\partial A1}{\partial Z1} &\times& \frac{\partial Z1}{\partial b1}\\ &&\\ \frac{\partial \hat{y}}{\partial b2}& = & \frac{\partial \hat{y}}{\partial Z2} &\times& \frac{\partial Z2}{\partial b2}\\ \end{matrix}\]

위의 공식을 비교해보면 각각 매개 변수에 동일하게 적용되는 미분이 있을 것이다. 이를 알고리즘으로 구현하여 좀 더 빠르게 미분값을 구할 수 있도록 고안한 것이 역전파 알고리즘이다.

역전파 알고리즘 미분 과정

역전파 알고리즘

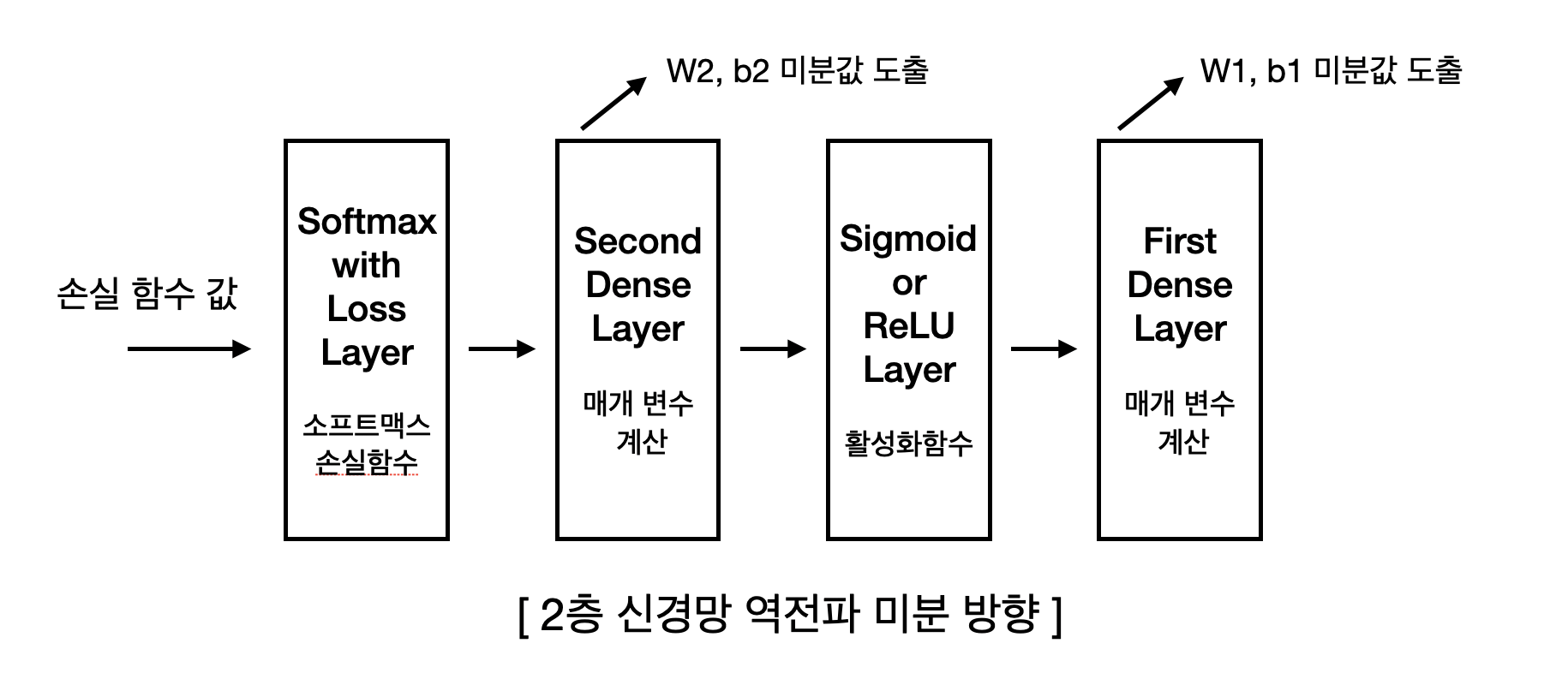
2층 신경망 역전파 알고리즘은 위와 같은 구조로 이루어져 있다. 우리는 위의 역전파 알고리즘에서 각 층을 함수로 구현할 것이다. 참고로 아래의 수식에서 사용되는 대문자는 행렬이며, 소문자는 스칼라이다. 특히 \(Z_n\)과 같은 기호는 행렬 \(Z\)의 \(n\)(인덱스)위치에 속해있는 요소를 가리킨다.

Softmax with Loss Layer

역전파 알고리즘에서는 출력층에서 사용되는 소프트맥스 함수와 손실 함수인 교차 엔트로피 오차 수식을 같이 미분한다. 그 이유는 두 함수를 동시에 미분한 결과가 훨씬 간단하기 때문이다. 역전파의 미분은 손실 함수인 교차 엔트로피 오차 수식 미분을 먼저 진행하고 그다음 소프트맥스 함수를 미분하여 결과를 도출할 것이다.

• 교차 엔트로피 오차 수식 미분

\[L = -\sum_{n} T_n \ln Y_n\]

위 식은 교차 엔트로피 오차이이며, \(T\)는 정답레이블, \(Y\)는 예측값, \(n\)은 신경망 노드의 개수를 의미한다. 즉, 소프트맥스 함수에서 예측값이 \([y_1, y_2, y_3]\)로 왔다면 \(n\)은 3이다. 위 식을 미분하면 다음과 같은 결과를 얻을 수 있다.

\[\partial L = -\sum_{n} \frac{T_n}{Y_n} \]

위의 식에서 \(-\frac{1}{Y_n}\)가 각각의 소프트맥스 함수의 신경망으로 전달된다. 예를 들어 소프트맥스 함수의 결과값이 총 3개가 들어왔다면 \(-\frac{T_1}{Y_1}, -\frac{T_2}{Y_2}, -\frac{T_3}{Y_3}\)이 소프트맥스 미분식의 입력값으로 들어간다.

• 소프트맥스 함수 미분

\[\sigma(Z_k)=\frac{e^{Z_k}}{\sum_{i=n}^n e^{Z_n}}\]

위 수식은 소프트맥스 함수이다. 위의 교차 엔트로피 오차와 마찬가지로 \(n\)은 신경망 노드 개수이다. 즉, 입력값이 \([z_1, z_2, z_3]\)이라면 \(n\)은 3이고, \(k\)는 \(1,2,3\) 중에 하나이다. 이를 미분하면 다음과 같은 결과를 얻을 수 있다.

1. 소프트맥스의 입력값과 편미분 대상이 동일할 때 (둘 다 \(Z_k\))

\[\frac{\partial\sigma(Z_k)}{\partial Z_k} = \frac{e^{Z_k}(\sum_{i} e^{Z_i})-e^{Z_k}e^{Z_k}}{(\sum_{i} e^{Z_i})^2}\]

\[\quad \quad \quad \ = \frac{e^{Z_k}\{(\sum_{i} e^{Z_i})-e^{Z_k}\}}{(\sum_{i} e^{Z_i})^2}\]

\[\quad \quad \quad \quad = \frac{e^{Z_k}}{\sum_{i} e^{Z_i}} \frac{(\sum_{i} e^{Z_i})-e^{Z_k}}{\sum_{i} e^{Z_i}}\]

\[\quad \quad \quad \quad = \frac{e^{Z_k}}{\sum_{i} e^{Z_i}}\Bigg(1-\frac{e^{Z_k}}{\sum_{i} e^{Z_i}}\Bigg)\]

\[\quad \quad = \sigma(Z_k)(1-\sigma(Z_k))\]

2. 소프트맥스의 입력값과 편미분 대상이 다를 때 (\(Z_k\)와 \(Z_j\))

\[\frac{\partial\sigma(Z_j)}{\partial Z_k} = \frac{0-e^{Z_k}e^{Z_j}}{(\sum_{i=1} e^{Z_i})^2}\]

\[\quad \quad \quad \quad \quad \quad \quad = -\frac{e^{Z_k}}{\sum_{i=1} e^{Z_i}} \frac{e^{Z_j}}{\sum_{i=1} e^{Z_i}}\]

\[\quad \quad \quad \quad = -\sigma(Z_k)\sigma(Z_j)\]

소프트맥스 함수는 미분될 때 동일한 변수와 동일하지 않은 변수를 모두 미분해야 한다. 그 이유는 손실 함수에서 \(n\)개의 변수를 미분하는데 \(n\)에는 편미분 변수인 \(k\)도 들어가지만 편미분 변수가 아닌 \(j\)도 포함되기 때문이다.

위의 미분식들을 활용하여 역전파 알고리즘에 사용되는 함수를 정리해보자.

\[\frac{\partial L}{\partial Z_k} = \frac{\partial L}{\partial \sigma(Z_n)}\frac{\partial\sigma(Z_n)}{\partial Z_k}\]

\[\quad \quad \ \ =-\sum_{n}\frac{Y_n}{Z_n}\frac{\partial\sigma(Z_n)}{\partial Z_k}\]

\(\frac{\partial\sigma(Z_n)}{\partial Z_k}\)은 \(k\)에 대한 미분과 \(j\)에 대한 미분을 모두 포함한다. 따라서 분리하여 미분을 진행한다.

\[\quad \quad \quad =-\frac{Y_k}{Z_k}Z_k(1-Z_k)-\sum_{n \ne k}\frac{Y_n}{Z_n}(-Z_kZ_n)\]

\[=-Y_k(1-Z_k)-\sum_{n \ne k}-Y_nZ_k\]

\[=-Y_k+Y_kZ_k+\sum_{n \ne k}Y_nZ_k\]

\[=-Y_k+Z_k\sum_{n}Y_n\]

여기서 \(\sum_{n}Y_n\)는 기존 소프트맥스 확률의 합이기 때문에 1이 된다.

\[=-Y_k+Z_k \times 1\]

\[=Z_k-Y_k\]

결론적으로 'Softmax with Loss'는 위와 같은 간단한 수식이다. 어차피 우리는 결론인 위의 간단한 수식만 사용할 것이기 때문에 만약 위의 수식들이 어렵다면 결론만 봐도 무방하다.

Dense Layer

'Dense Layer'는 들어온 입력값에 가중치를 곱하고 편향을 더하는 방정식이다. 수식으로 쓰면 아래와 같다.

\[Z=XW+B\]

위 수식을 미분해보자. 참고로 Dense Layer에서 사용되는 모든 변수들은 행렬을 기본으로 하고 있다. 즉, \(XW\)은 행렬곱이다. 그렇다면 행렬곱은 어떻게 미분되는가? 기본적으로 신경망에서 사용되는 행렬은 벡터 단위이다. 즉, 행렬도 벡터가 여러 개 합쳐져 있는 형태로 바라본다는 것이다.

미분을 이해하기 위해서 간단하게 예시를 보자.

입력값인 행렬 \(X\)와 가중치인 행렬 \(W\)를 다음과 같이 설정한다. 벡터는 열벡터 형태가 기본이기 때문에 아래의 행렬은 벡터 별 색깔을 다르게 설정하였다. \[\begin{matrix} \quad \quad X_1 & X_2 &&&& W_1 & W_2 &W_3 \end{matrix}\] $$X= \[\begin{bmatrix} \color{ForestGreen}{x_{11}} &\color{LimeGreen}{x_{12}}\\ \color{ForestGreen}{x_{21}} & \color{LimeGreen}{x_{22}} \end{bmatrix}\] W= \[\begin{bmatrix} \color{OrangeRed}{w_{11}} & \color{Orange}{w_{12}} & \color{Salmon}{w_{13}}\\ \color{OrangeRed}{w_{21}} & \color{Orange}{w_{22}} & \color{Salmon}{w_{23}} \end{bmatrix}\]

$$

두 행렬을 곱할 때는 열 단위로 내적되는 것이 아니라 X가 행벡터로 변환되어 내적된다. 즉, 수식으로 표현하면 다음과 같다.

\[X \cdot W = X^TW\]

따라서 \(X \cdot W\)인 식이 결과값 \(Y\)라고 했을 때, \(Y\)는 다음과 같다.

\[Y=\begin{bmatrix} \color{ForestGreen}{x_{11}}\color{OrangeRed}{w_{11}}+ \color{ForestGreen}{x_{21}}\color{OrangeRed}{w_{21}}& \color{ForestGreen}{x_{11}}\color{Orange}{w_{12}} +\color{ForestGreen}{x_{21}}\color{Orange}{w_{22}}& \color{ForestGreen}{x_{11}}\color{Salmon}{w_{13}}+\color{ForestGreen}{x_{21}}\color{Salmon}{w_{23}}\\ \color{LimeGreen}{x_{12}}\color{OrangeRed}{w_{11}}+ \color{LimeGreen}{x_{22}}\color{OrangeRed}{w_{21}}& \color{LimeGreen}{x_{12}}\color{Orange}{w_{12}}+ \color{LimeGreen}{x_{22}}\color{Orange}{w_{22}}& \color{LimeGreen}{x_{12}}\color{Salmon}{w_{13}}+\color{LimeGreen}{x_{22}}\color{Salmon}{w_{23}} \end{bmatrix}\]

위의 행렬을 벡터의 곱으로 표현해보자.

\[Y=\begin{bmatrix} X_1W_1 & X_1W_2 & X_1W_3\\ X_2W_1 & X_2W_2 & X_2W_3\\ \end{bmatrix}\]

위 식은 행렬 \(W\)가 행렬 \(X^T\)와 곱한 형태라는 것을 증명한다. 위의 행렬을 \(W_1~ or~ W_2~ or~ W_3\)로 각각 미분해도 결과는 동일하다.

\[\frac{\partial Y}{\partial W} = \begin{bmatrix} X_1\\ X_2\\ \end{bmatrix}\]

이를 행렬로 풀면 다음과 같다.

\[\frac{\partial Y}{\partial W} = \begin{bmatrix} \color{ForestGreen}{x_{11}} &\color{ForestGreen} {x_{21}}\\ \color{LimeGreen}{x_{12}} & \color{LimeGreen}{x_{22}}\\ \end{bmatrix} = X^T\]

위와 같은 원리로 다음과 같은 결론을 낼 수 있다.

\[\frac{\partial Y}{\partial W} = X^T\] \[\frac{\partial Y}{\partial X} = W^T\]

우리는 역전파 알고리즘에서 입력값과 가중치의 미분값으로 위의 식을 사용할 것이다.

편향의 경우, 신경망 계산 시에 모든 원소에 더해지기 때문에 미분값을 열 기준으로 전부 더하면 된다.

Sigmoid Layer

시그모이드 함수의 미분은 간단하다. 아래의 식을 확인하자.

\[\frac{\partial h(Z_k)}{\partial Z_k} = \frac{0\times(1+e^{-Z_k})-1\times (0+e^{(-Z_k)})(-1) }{(1+e^{-Z_k})^2}\]

\[\quad =\frac{e^{(-Z_k)}}{(1+e^{-Z_k})^2}= \frac{1+e^{(-Z_k)}-1}{(1+e^{-Z_k})^2}\]

\[=\frac{(1+e^{(-Z_k)})}{(1+e^{-Z_k})^2}-\frac{1}{(1+e^{-Z_k})^2}\]

\[= \frac{1}{(1+e^{-Z_k})}-\frac{1}{(1+e^{-Z_k})^2}\]

\[\quad = \frac{1}{(1+e^{-Z_k})}\Big(1-\frac{1}{(1+e^{-Z_k})}\Big)\]

\[ = h(Z_k)(1-h(Z_k))\]

시그모이드 함수를 미분하여 정리하면 \(h(Z_k)(1-h(Z_k))\) 이 도출된다. 따라서 역전파 알고리즘에 사용되는 시그모이드 함수는 위의 수식을 사용하여 구현될 것이다.

ReLU Layer

ReLU 함수는 입력값 \(x\)가 음수인 경우만 0으로 변경하고 그대로 출력한다. 이를 수식으로 표현하면 다음과 같다.

\[ y = \begin{cases} 0 & \text{(x≤0)\]}\ x & \ \end{cases} $$

위 수식을 입력값 \(x\)로 미분하면 아래와 같은 결과가 도출된다.

\[ \frac{\partial y}{\partial x} = \begin{cases} 0 & \text{(x≤0)\]}\ 1 & \ \end{cases} $$

따라서 역전파 알고리즘에서 Relu 함수는 입력값 \(x\)가 0보다 같거나 작으면 미분값에 0을 곱해서 출력하고, \(x\)보다 크면 1을 곱해서 출력한다. 그렇기 때문에 입력값에서 음수의 위치를 저장해두어야 한다.

순전파 vs. 역전파

다음 글에서 살펴볼 역전파 알고리즘이 과연 잘 구현되었는지 확인해보자. 먼저 훈련데이터 이미지 3개를 x_batch와 t_batch에 할당한다. (참고로 사용된 훈련데이터는 MNIST 데이터이며, 이전 글에서 가져오는 방법을 볼 수 있다.)

x_batch = train_x[1:3, :]
t_batch = t[1:3, :]

그 다음 순전파 알고리즘을 먼저 작동해보자.

TwoLayerNet_numerical_gradient(loss, x_batch, t_batch)

위 코드를 실행하면 순전파 알고리즘으로부터 도출된 미분값을 얻을 수 있다.

grad_forward_W1 = grads["W1"]
grad_forward_b1 = grads["b1"]
grad_forward_W2 = grads["W2"]
grad_forward_b2 = grads["b2"]

위 코드를 입력하여 미분값을 저장하자. 이제 역전파 알고리즘을 사용하여 매개 변수의 미분값을 얻으려 한다. 역전파 알고리즘은 아직 살펴보지 못했기에 그 결과를 아래의 식에 도입해서 확인해보자.

\[Difference = \frac{\sum{|forward~gradient - backward~gradient|}}{the~number~of~elements~in~Matrix}\]

위 식을 코드로 구현하면 아래와 같다.

Julia> diffW1 = sum((abs.(grad_forward_W1-grad_backward_W1))) / (size(grad_backward_W1)[1]*size(grad_backward_W1)[2])
Julia> diffW2 = sum((abs.(grad_forward_W2-grad_backward_W2))) / (size(grad_backward_W2)[1]*size(grad_backward_W2)[2])
Julia> diffb1 = sum((abs.(grad_forward_b1-grad_backward_b1))) / (size(grad_backward_b1)[1]*size(grad_backward_b1)[2])
Julia> diffb2 = sum((abs.(grad_forward_b2-grad_backward_b2))) / (size(grad_backward_b2)[1]*size(grad_backward_b2)[2])

위 코드는 다음 글에서 역전파 알고리즘을 구현한 후 작동할 것이다. 결과는 다음과 같다.

Julia> diffW1
 1.9589789748798898e-10
Julia> diffW2
 7.040410144965037e-8
Julia> diffb1
 8.881836618344343e-10
Julia> diffb2
 1.394640827490079e-7

순전파와 역전파 알고리즘으로 도출된 미분값들의 차이가 매우 작은 것을 확인할 수 있다. 즉, 역전파가 잘 구현되었다는 것이다. 그렇다면 역전파는 어떻게 줄리아로 구현하였을까? 다음 글에서 확인해보자.